材料1.类比是获取数学知识的重要思想之一,很多优美的数学结论就是利用类比思想获得的.例如:若a>0,b>0,则a+b2≥ab,当且仅当a=b时,取等号,我们称为二元均值不等式.类比二元均值不等式得到三元均值不等式:a>0,b>0,c>0,则a+b+c3≥3abc,当且仅当a=b=c时,取等号.我们经常用它们求相关代数式或几何问题的最值,某同学做下面几何问题就是用三元均值不等式圆满完成解答的.
题:将边长为12cm的正方形硬纸片(如图1)的四个角裁去四个相同的小正方形后,折成如图2的无盖长方体小纸盒,求纸盒容积的最大值.
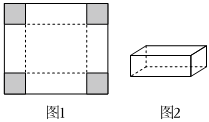
解:设截去的小正方形的边长为x(0<x<6),则纸盒容积V=(12-2x)2x=14(12-2x)(12-2x)(4x)≤14(12-2x+12-2x+4x3)3=128.
当且仅当12-2x=12-2x=4x,即x=2时取等号.所以纸金的容积取得最大值128cm3.在求V的最大值中,用均值不等式求最值时,遵循“一正二定三相等”的规则.你也可以将V=(12-2x)2x变形为V=(12-2x)2x=2(6-x)(6-x)(2x)求解.
你还可以设纸盒的底面边长为a,高为b,则a+2b=12,则纸盒容积V=a2b=14aa(4b)≤14(a+a+4b3)3=14×(2(a+2b)3)3=14×(2×123)3=128.
当且仅当a=a=4b,即a=8,b=2时取等号,所以纸盒的容积取得最大值128cm3.
材料2.《数学必修二》第八章8.3节习题8.3设置了如下第4题:
如图1,圆锥的底面直径和高均为a,过PO的中点O1作平行于底面的截面,以该截面为底的面挖去一个圆柱,求剩下几何体的表面积和体积.我们称圆柱为圆锥的内接圆柱.
根据材料1与材料2完成下列问题.
如图2,底面直径和高均为6cm的圆锥有一个底面半径为R,高为H的内接圆柱.
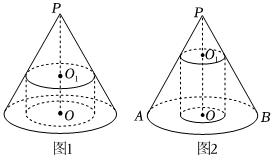
(1)求R与H的关系式;
(2)求圆柱侧面积的最大值;
(3)求圆柱体积的最大值.
a
+
b
2
≥
ab
a
+
b
+
c
3
≥
3
abc
1
4
(
12
-
2
x
)
(
12
-
2
x
)
(
4
x
)
≤
1
4
(
12
-
2
x
+
12
-
2
x
+
4
x
3
)
3
1
4
aa
(
4
b
)
≤
1
4
(
a
+
a
+
4
b
3
)
3
=
1
4
×
(
2
(
a
+
2
b
)
3
)
3
=
1
4
×
(
2
×
12
3
)
3
【答案】(1)2R+H=6;
(2)9πcm2;
(3)8πcm3.
(2)9πcm2;
(3)8πcm3.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/5/25 8:0:9组卷:77引用:2难度:0.5
相似题
-
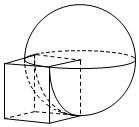 1.如图,将半径为1的球与棱长为1的正方体组合在一起,使正方体的一个顶点正好是球的球心,则这个组合体的体积为( )发布:2024/10/6 12:0:1组卷:480引用:7难度:0.7
1.如图,将半径为1的球与棱长为1的正方体组合在一起,使正方体的一个顶点正好是球的球心,则这个组合体的体积为( )发布:2024/10/6 12:0:1组卷:480引用:7难度:0.7 -
 2.如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°.
2.如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°.
(Ⅰ)求证:AC⊥BM;
(Ⅱ)求二面角M-AB-C的大小;
(Ⅲ)求多面体PMABC的体积.发布:2024/6/27 10:35:59组卷:303引用:5难度:0.1 -
 3.如图,在矩形ABCD中,E为边AD的中点,AB=1,BC=2,分别以A、D为圆心,1为半径作圆弧、ˆEB(E在线段AD上).由两圆弧ˆEC、ˆEB及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的体积为 .ˆEC发布:2024/6/27 10:35:59组卷:343引用:5难度:0.7
3.如图,在矩形ABCD中,E为边AD的中点,AB=1,BC=2,分别以A、D为圆心,1为半径作圆弧、ˆEB(E在线段AD上).由两圆弧ˆEC、ˆEB及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的体积为 .ˆEC发布:2024/6/27 10:35:59组卷:343引用:5难度:0.7


