当前位置：试卷中心 > 试卷详情

2022-2023学年广西玉林市高一（下）期末数学试卷

发布：2024/6/8 8:0:9

一、单项选择题（共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）

1．
2
+
i
1
-
i
=（　　）
A．
1
2
+
3
2
i
B．
-
1
2
+
3
2
i
C．
1
2
-
3
2
i
D．
-
1
2
-
3
2
i
组卷：15引用：1难度：0.8
解析
2．在以下调查中，适合用全面调查的是（　　）
A．调查一个县各村的粮食播种面积
B．调查一批玉米种子的发芽率
C．调查一批炮弹的杀伤半径
D．调查一个水库所有鱼中草鱼所占的比例．
组卷：184引用：6难度：0.7
解析
3．若四边形ABCD满足
AB
+
CD
=
0
，（
AB
-
AD
）•
AC
=0，则该四边形一定是（　　）
A．直角梯形 B．矩形 C．菱形 D．正方形
组卷：589引用：54难度：0.9
解析
4．如图为2022年北京冬奥会首钢滑雪大跳台示意图，为测量大跳台最高点P距地面的距离，小明同学在场馆内的A点测得P的仰角为30°，∠ABO=120°，∠BAO=30°，AB=60（单位：m），（点A，B，O在同一水平地面上），则大跳台最高高度OP=（　　）
A．45m B．
45
2
m
C．60m D．
60
3
m
组卷：82引用：7难度：0.7
解析
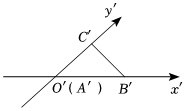5．用斜二测画法作出△ABC的水平放置的直观图△A′B′C′如图所示，其中
A
′
C
′
=
3
，
A
′
B
′
=
1
，则△ABC绕AC所在直线旋转一周后所形成的几何体的表面积为（　　）
A．
5
3
π
B．2π C．3π D．
（
13
+
1
）
π
组卷：30引用：1难度：0.8
解析
6．一个盒子里装有标号为1，2，3，4，5的5张标签，无放回的随机选取两张标签，则两张标签上的数字为相邻整数的概率是（　　）
A．
1
5
B．
2
5
C．
3
5
D．
4
5
组卷：20引用：3难度：0.9
解析
7．已知m,n是两条不同的直线，α，β是两个不同的平面，则以下命题正确的是（　　）
A．若m∥n,m∥α，n∥β，则α∥β B．若m⊥n,m⊥α，则n∥α
C．若m∥α，m⊥n,则n⊥α D．若m⊥α，m∥β，则α⊥β
组卷：48引用：4难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（共6小题，其中第17题10分，其他每题12分，共70分.解答应写出文字说明、证明过程或演算步骤.）

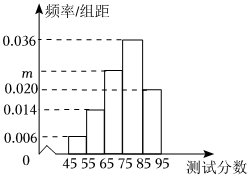20．某学校为了了解高二年级学生数学运算能力，对高二年级的300名学生进行了一次测试．已知参加此次测试的学生的分数x_i（i=1，2，⋯，300）全部介于45分到95分之间，该校将所有分数分成5组：[45，55），[55，65），⋯，[85，95]，整理得到如下频率分布直方图（同组数据以这组数据的中间值作为代表）．
（1）求m的值，并估计此次校内测试分数的平均值
x
；
（2）学校要求按照分数从高到低选拔前30名的学生进行培训，试估计这30名学生的最低分数；
（3）试估计这300名学生的分数x_i（i=1，2，⋯，300）的方差s²，并判断此次得分为52分和94分的两名同学的成绩是否进入到了
[
x
-
2
s
,
x
+
2
s
]
范围内？
（参考公式：
s
2
=
1
n
n
∑
i
=
1
f
i
（
x
i
-
x
）
2
，其中f_i为各组频数；参考数据：
129
≈
11
.
4
）
组卷：35引用：1难度：0.5
解析
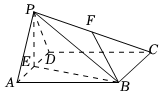21．如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠BAD=60°，△PAD是正三角形，E为线段AD的中点，点F为棱PC上的动点．
（1）求证：平面PBC⊥平面PBE；
（2）若平面PAD⊥平面ABCD．
①当点F恰为PC中点时，求异面直线PD与BF所成角的余弦值；
②在平面PBE内确定一点H，使CH+FH的值最小，并求此时
BH
BP
的值．
组卷：203引用：5难度：0.5
解析