2023-2024学年云南省三校高三（上）第二次联考数学试卷

一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知集合M={-2，-1，0，1，2，3}，N={x|x²-x-6≥0}，则M∩N=（　　）

  A．{-2，3}

  B．{0，1，2}

  C．{-2，-1，0，1}

  D．{2}
  组卷：42引用：2难度：0.7

  解析

• 2．若复数（a-i）（1+ai）=2，a∈R，则a=（　　）

  A．-1

  B．0

  C．1

  D．2
  组卷：24引用：3难度：0.7

  解析

• 3．已知

  sinαcosα

  =

  1

  8

  ，且

  π

  4

  ＜

  α

  ＜

  π

  2

  ，则下列结果正确的是（　　）

  A． sin 2 α = 1 8	B． sinα + cosα = 5 2
  C． sinα - cosα = - 3 2	D． tanα = 4 - 15
  组卷：77引用：3难度：0.6

  解析

• 4．记S_n为等差数列{a_n}的前n项和．若a₁+a₃+a₈=15，a₄a₈=45，则S₅=（　　）

  A．25

  B．22

  C．20

  D．15
  组卷：109引用：2难度：0.7

  解析

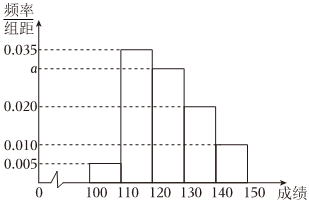• 5．要调查某地区高中学生身体素质，从高中生中抽取100人进行跳高测试，根据测试成绩制作频率分布直方图如图，现从成绩在[120，140）之间的学生中用分层抽样的方法抽取5人，应从[120，130）间抽取人数为b,则（　　）

  A．a=0.2，b=2	B．a=0.025，b=3
  C．a=0.3，b=4	D．a=0.030，b=3
  组卷：604引用：5难度：0.7

  解析

• 6．已知直线y=2x与圆（x-2）²+（y-2）²=1交于A，B两点，则|AB|=（　　）

  A． 5 5

  B． 2 5 5

  C． 3 5 5

  D． 4 5 5
  组卷：148引用：2难度：0.7

  解析

• 7．基本再生数R₀与世代间隔T是新冠肺炎的流行病学基本参数．基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间．在新冠肺炎疫情初始阶段，可以用指数模型：I（t）=e^rt描述累计感染病例数I（t）随时间t（单位：天）的变化规律，指数增长率r与R₀，T近似满足R₀=1+rT．有学者基于已有数据估计出R₀=3.28，T=6．据此，在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间约为（　　）（ln2≈0.69）

  A．1.2天

  B．1.8天

  C．2.5天

  D．3.5天
  组卷：4345引用：44难度：0.5

  解析

四、解答题（共70分，解答应写出文字说明，证明过程或演算步骤）

• 21．已知g（x）=xe^x-a（lnx+x）．
  （1）当a=1时，求g（x）在（1，+∞）上的单调性；
  （2）若h（x）=xe^x，令f（x）=h′（x），讨论方程f（x）=m（m∈R）的解的个数．
  组卷：19引用：2难度：0.5

  解析

• 22．已知圆A₁：（x+1）²+y²=16，直线l₁过点A₂（1，0）且与圆A₁交于点B，C，线段BC的中点为D，过A₂C的中点E且平行于A₁D的直线交A₁C于点P．
  （1）求动点P的轨迹方程；
  （2）坐标原点O关于A₁，A₂的对称点分别为B₁，B₂，点A₁，A₂关于直线y=x的对称点分别为C₁，C₂，过A₁的直线l₂与动点P的轨迹交于点M，N，直线B₁M与B₂N相交于点Q．求证：△QC₁C₂的面积是定值．
  组卷：39引用：2难度：0.5

  解析