2022-2023学年陕西省西安市鄠邑区高二（下）期末数学试卷（文科）

一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）

• 1．若a∈R，z满足z（1+i）=a+2i,且z为纯虚数，则a=（　　）

  A．1

  B．-1

  C．2

  D．-2
  组卷：53引用：2难度：0.9

  解析

• 2．已知点M的直角坐标为（-1，-

  3

  ，3），则它的柱坐标是（　　）

  A．（2， π 3 ，3）

  B．（2， 2 π 3 ，3）

  C．（2， 4 π 3 ，3）

  D．（2， 5 π 3 ，3）
  组卷：161引用：4难度：0.9

  解析

• 3．若椭圆的参数方程为

  x = 2 cosφ

  y = 3 sinφ

  （φ为参数），则该椭圆的离心率为（　　）

  A． 1 2

  B． 3 2

  C． 2 2

  D． 3 4
  组卷：372引用：3难度：0.8

  解析

• 4．用反证法证明命题“平面四边形四个内角中至少有一个不大于90°”时，应假设（　　）

  A．四个内角都大于90°

  B．四个内角都不大于90°

  C．四个内角至多有一个大于90°

  D．四个内角至多有两个大于90°
  组卷：89引用：4难度：0.8

  解析

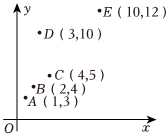• 5．有一散点图如图所示，在5个数据（x,y）中去掉D（3，10）后，下列说法正确的是（　　）

  A．相关系数r变小

  B．残差平方和变小

  C．变量x,y负相关

  D．解释变量x与预报变量y的相关性变弱
  组卷：36引用：7难度：0.7

  解析

• 6．一组成对数据（x₁，y₁），（x₂，y₂），（x₃，y₃），⋯，（x_n，y_n）样本中心点为

  （

  x

  ，

  y

  ）

  （

  x

  =

  1

  n

  n

  ∑

  i

  =

  1

  x

  i

  ，

  y

  =

  1

  n

  n

  ∑

  i

  =

  1

  y

  i

  ）

  ，由这组数据拟合的线性回归方程为

  ̂

  y

  =

  a

  +

  bx

  ，用最小二乘法求回归方程是为了使（　　）最小．

  A．总偏差平方和 n ∑ i = 1 （ y i - y ） 2

  B．残差平方和 n ∑ i = 1 （ y i - ̂ y i ） 2

  C．回归平方和 n ∑ i = 1 （ ̂ y i - y ） 2

  D．竖直距离和 n ∑ i = 1 | y i - ̂ y i |
  组卷：52引用：1难度：0.5

  解析

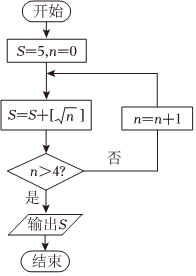• 7．[x]表示不超过x的最大整数，执行如图所示的程序框图，则输出的S值为（　　）

  A．6

  B．9

  C．10

  D．13
  组卷：3引用：1难度：0.8

  解析

三、解答题（本大题共6小题，满分70分，解答应写出必要的文字说明、证明过程或演算步骤.）

• 21．（1）用分析法证明：（a²+b²）（c²+d²）≥（ac+bd）²（当且仅当ad=bc时等号成立）．
  （2）设M（a,n）=|ax-1|+|ax-2|+⋯+|ax-n|为曼哈顿扩张距离，其中n为正整数．如M（2，6）=|2x-1|+|2x-2|+|2x-3|+|2x-4|+|2x-5|+|2x-6|．若M（1，2）≥m对一切实数x恒成立．设a＞0，b＞0，且a²+b²=m_max+1，求证：a+b≤2．
  组卷：11引用：1难度：0.4

  解析

• 22．以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=8cosθ+6sinθ，圆C与极轴交于点A（异于坐标原点O），点B是圆C上的任意一点．
  （1）写出点A的极坐标和圆C的参数方程；
  （2）求

  OC

  •

  AB

  的最大值．
  组卷：10引用：1难度：0.5

  解析