2023-2024学年浙江省七彩阳光新高考研究联盟高三(上)返校数学试卷
发布:2024/8/12 19:0:1
一、单项选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1.已知集合
,则A∩B=( )A={α|0<α<π},B={β|β=kπ3+π2,k∈Z}组卷:19引用:1难度:0.9 -
2.在复平面内,复数z对应的点在第一象限,i为虚数单位,则复数zi对应的点位于( )
组卷:17引用:2难度:0.7 -
3.已知向量
,在直线l方向向量上的投影向量相等,则直线l的斜率为( )a=(1,2),b=(3,4)组卷:207引用:8难度:0.8 -
4.若双曲线的两个顶点将两焦点间的线段三等分,则该双曲线的离心率为( )
组卷:128引用:1难度:0.8 -
5.过圆O:x2+y2=9上一点P作圆M:(x-1)2+(y-1)2=1的两条切线PA,PB,切点为A,B.当∠APB最大时,直线AB的斜率为( )
组卷:149引用:2难度:0.7 -
6.若函数y=f(2x+1)+1为奇函数,则( )
组卷:137引用:1难度:0.7 -
7.已知
,且α∈(0,π2),则cosα=( )32sin(2α+π3)-sin(α+π3)=-34组卷:71引用:1难度:0.6
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
-
21.已知数列{an}和{bn}满足
.a1=1,an+1=an+2bnn,b1+12b2+13b3+⋯+1nbn=an(n∈N*)
(1)求an与bn;
(2)设数列{bn}的前n项和为Sn,是否存在实数λ,μ,使得λan,Sn,μbn成等差数列?若存在求出λ,μ的值;若不存在,请说明理由.组卷:85引用:1难度:0.5 -
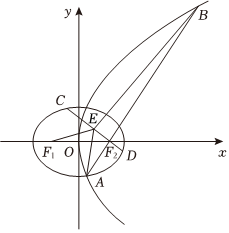 22.如图,已知椭圆的左,右焦点分别为F1,F2,抛物线y2=4mx的焦点为F2,抛物线的弦AB和椭圆的弦CD交于点F2,且AB⊥CD,E为CD的中点.x22+y2=m
22.如图,已知椭圆的左,右焦点分别为F1,F2,抛物线y2=4mx的焦点为F2,抛物线的弦AB和椭圆的弦CD交于点F2,且AB⊥CD,E为CD的中点.x22+y2=m
(1)求m的值;
(2)记△ABE的面积为S1,△F1EF2的面积为S2,求的最小值.S1S2组卷:68引用:1难度:0.5


