当前位置：试卷中心 > 试卷详情

2022-2023学年山西省大同三中九年级（上）月考数学试卷（12月份）

发布：2024/8/20 7:0:4

一、选择题（本题共计10小题，每题3分，共计30分）

1．已知二次函数y=3（x-1）²+5，下列结论正确的是（　　）
A．其图象的开口向下
B．图象的对称轴为直线x=-1
C．函数的最大值为5
D．当x＞1时，y随x的增大而增大
组卷：445引用：14难度：0.7
解析
2．将抛物线y=（x-1）²+4先向右平移4个单位长度，再向下平移3个单位长度，得到的抛物线的顶点坐标为（　　）
A．（5，4） B．（1，4） C．（1，1） D．（5，1）
组卷：119引用：3难度：0.7
解析
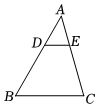3．已知：如图，在△ABC中，DE∥BC，AD：DB=1：2，S_△ADE=2，则S_{四边形BCED}大小为（　　）
A．4 B．8 C．16 D．18
组卷：26引用：2难度：0.6
解析
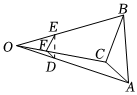4．如图，已知△ABC，任取一点O，连AO，BO，CO，分别取点D，E，F，使OD=
1
3
AO，OE=
1
3
BO，OF=
1
3
CO，得△DEF．下列说法中，错误的是（　　）
A．△DEF与△ABC是位似三角形
B．△OAC与△ODF是位似三角形
C．△DEF与△ABC周长的比是1：3
D．图中位似的两个三角形面积比是1：9
组卷：176引用：2难度：0.6
解析
5．如图，△ABC内接于⊙O，AB为⊙O直径，点D是⊙O上的一点（点C，D在AB的两侧），连接AD，CD．若∠BAC=36°，则∠ADC=（　　）
A．36° B．54° C．64° D．72°
组卷：272引用：3难度：0.6
解析
6．如图，已知点A（3，6）、B（1，4）、C（1，0），则△ABC外接圆的圆心坐标是（　　）
A．（0，0） B．（2，3） C．（5，2） D．（1，4）
组卷：541引用：4难度：0.7
解析
7．用配方法解方程x²-2x-2=0时，配方后所得的方程为（　　）
A．（x+2）²=1 B．（x-2）²=3 C．（x-1）²=1 D．（x-1）²=3
组卷：33引用：2难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共计8小题，共计75分）

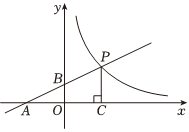22．如图，直线y=ax+1与x轴，y轴分别相交于A，B两点，与双曲线
y
=
k
x
（
x
＞
0
）
相交于点P，PC⊥x轴于点C，且PC=2，点A的坐标为（-2，0）．
（1）求双曲线的解析式；
（2）若点Q为双曲线上点P右侧的一点，且QH⊥x轴于H，当以点Q，C，H为顶点的三角形与△AOB相似时，求点Q的坐标；
（3）点M为y轴上一点，当以点M，A，P为顶点的三角形是直角三角形时，请直接写出点M的坐标．
组卷：109引用：2难度：0.5
解析
23．如图，在平面直角坐标系xOy中，下表给出了抛物线y=ax²+bx+c上部分点（x,y）的坐标值：

x … -1
1
2
0
3
2
…

y … 0 3 3 0 …

（1）求抛物线的解析式；
（2）如图，直线y=-2x+3与抛物线交于B、C两点，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标和△BEC面积的最大值？
（3）如图：A为抛物线与x轴的一个交点，在（2）的结论下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．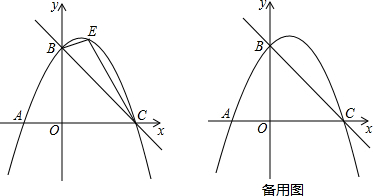
组卷：253引用：3难度：0.4
解析