2021-2022学年浙江省宁波市慈溪市科学中学七年级（下）期中数学试卷

一、选择题（每题3分，共30分）

• 1．下列运算正确的是（　　）

  A．a3+a3=a6	B．（-a2）3•a6=a12
  C．2a6÷a3=2a2	D．2a3•3a5=6a8
  组卷：20引用：1难度：0.7

  解析

• 2．新冠病毒是一种新的β属冠状病毒，它的平均直径为0.000000085m,其中，0.000000085用科学记数法可以表示为（　　）

  A．8.5×10-8

  B．8.5×10-7

  C．85×10-8

  D．85×10-7
  组卷：11引用：1难度：0.8

  解析

• 3．若4a²+kab+9b²为一个完全平方式，则k的值为（　　）

  A．6

  B．±6

  C．12

  D．±12
  组卷：122引用：2难度：0.7

  解析

• 4．64-（3a-2b）²分解因式的结果是（　　）

  A．（8+3a-2b）（8-3a-2b）	B．（8+3a+2b）（8-3a-2b）
  C．（8+3a+2b）（8-3a+2b）	D．（8+3a-2b）（8-3a+2b）
  组卷：247引用：2难度：0.7

  解析

• 5．下列各式中，正确的是（　　）

  A．- - 3 x 5 y = 3 x - 5 y	B．- a + b c = - a + b c
  C．- a b - a = a a - b	D． - a - b c = a - b - c
  组卷：483引用：5难度：0.7

  解析

• 6．如果分式

  6

  x

  -

  1

  的值是整数，则整数x可取的值的个数是（　　）

  A．10个

  B．8个

  C．6个

  D．4个
  组卷：152引用：3难度：0.7

  解析

• 7．“五一”前夕，某校社团进行爱心义卖活动，先用800元购进第一批康乃馨，包装后售完，接着又用400元购进第二批康乃馨，已知第二批所购数量是第一批所购数量的

  1

  3

  ，且康乃馨的单价比第一批的单价多1元，设第一批康乃馨的单价是x元，则下列方程正确的是（　　）

  A． 1 3 × 800 x = 400 x + 1	B． 800 x = 1 3 × 400 x + 1
  C． 800 x +1= 400 x	D． 800 x = 400 x + 1 +1
  组卷：34引用：2难度：0.7

  解析

三、解答题（第17、18题每题8分，第19题10分，第20题8分，第21题10分，第22题10分，第23题12分，共66分）

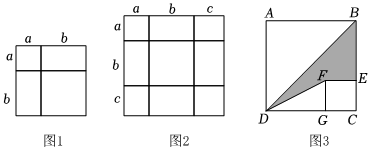• 22．用几个小的长方形、正方形拼成一个大的正方形，然后利用两种不同的方法计算这个大的正方形的面积，可以得到一个等式．例如：计算图1的面积，把图1看作一个大正方形，它的面积是（a+b）²；如果把图1看作是由2个长方形和2个小正方形组成的，它的面积为a²+2ab+b²，由此得到（a+b）²=a²+2ab+b²．
  （1）如图2，由几个面积不等的小正方形和几个小长方形拼成一个边长为（a+b+c）的正方形，从中你能发现什么结论？该结论用等式表示为

  ；
  （2）利用（1）中的结论解决以下问题：已知a+b+c=10，ab+ac+bc=38，求a²+b²+c²的值；
  （3）如图3，由正方形ABCD边长为a,正方形CEFG边长为b,点D，G，C在同一直线上，连接BD，DF，若a-b=2，ab=3，求图3中阴影部分的面积．
  组卷：676引用：5难度：0.4

  解析

• 23．定义：若一个正整数能表示成a²-b²（a,b是正整数）的形式，我们把这个正整数叫做“平方差数”．例如20是“平方差数”，理由：20=6²-4²，所以20是“平方差数”．
  解决问题：
  （1）请写出一个小于10的“平方差数”，这个“平方差数”为

  ；
  （2）判断36

  （填“是”或“不是”）“平方差数”；
  探究问题：
  （3）已知M=x²+6x+k（x是正整数，k为大于0是常数），是否存在k使得M为“平方差数”，若存在，请求出k的值；若不存在，请说明理由．
  （4）如果数m,n都是“平方差数”，请说明mn也是“平方差数”．
  组卷：137引用：1难度：0.5

  解析