2023-2024学年北京市西城区德胜中学八年级（上）期中数学试卷
发布：2024/9/25 11:0:6
一、选择题（下列各题均有四个选项，其中只有一个是符合题意的）
-
1．下列几种著名的数学曲线中，不是轴对称图形的是（ ）
组卷：213引用：8难度：0.9 -
2．画△ABC的高BE，以下画图正确的是（ ）
组卷：630引用：10难度：0.9 -
3．一个多边形内角和是1080°，则这个多边形是（ ）
组卷：577引用：74难度：0.9 -
4．李老师在“数学嘉年华”活动中组织学生用小棍摆三角形，小棍的长度有8cm,12cm,16cm和20cm四种规格，小明同学已经取了8cm和12cm两根木棍，那么第三根木根不可能取（ ）
组卷：122引用：6难度：0.7 -
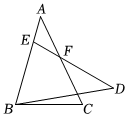5．如图，已知△ABC≌△DEB，点E在AB上，若∠A=40°，∠DBE=65°，则∠AED的度数为（ ）组卷：166引用：3难度：0.5 -
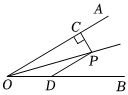6．如图，点P在∠AOB的平分线上，PC⊥OA于点C，PD∥OA，交OB于点D，∠AOB=30°，且OD=4．则线段PC的长度为（ ）组卷：75引用：3难度：0.5 -
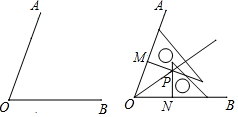7．小明在没有量角器和圆规的情况下，利用刻度尺和一副三角板画出了一个角的平分线，他的做法是这样的：如图，（1）利用刻度尺在∠AOB的两边OA，OB上分别取OM=ON；（2）利用两个三角板，分别过点M，N画OM，ON的垂线，交点为P；（3）画射线OP．则射线OP为∠AOB的平分线．小明这种画法的依据（ ）组卷：170引用：5难度：0.5 -
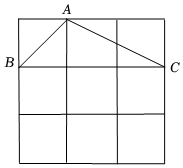8．在如图所示的3×3网格中，△ABC是格点三角形（即顶点恰好是网格线的交点），则与△ABC有一条公共边且全等（不含△ABC）的所有格点三角形的个数是（ ）组卷：322引用：3难度：0.5
三、解答题
-
24．阅读理解
半角模型：半角模型是指有公共顶点，锐角等于较大角的一半，且组成这个较大角两边相等，通过翻折或旋转，将角的倍分关系转化为角的相等关系，并进一步构造全等三角形，使条件弱化，这样可把握问题的本质．【问题背景】
如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且∠EAF=60°，试探究图1中线段BE、EF、FD之间的数量关系．
【初步探索】
小亮同学认为解决此问题可以用如下方法：延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，则可得到线段BE、EF、FD之间的数量关系是 ．
【探索延伸】
如图2，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC、CD上的点，，上述结论是否仍然成立，并说明理由．∠EAF=12∠BAD
【结论运用】
如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进，1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E、F处；且两舰艇之间的夹角∠EOF为70°，则此时两舰艇之间的距离为 海里．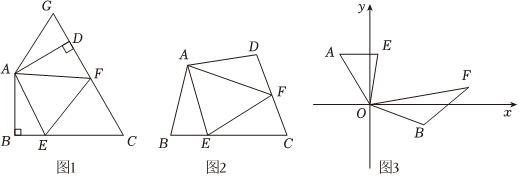
组卷：315引用：5难度：0.5 -
25．点P为平面内任意一点，若△ABC上存在点Q，满足PQ=1，则称点P为△ABC的等距离点．在平面直角坐标系xOy中，点A（t-4，1）与点B关于过点（t,0）且垂直于x轴的直线对称．
（1）以AB为底边作等腰△ABC，
①t=0，点B的坐标为 ；
②当t=1，且底边AB上的高为3时，点C的坐标为 ．
（2）以AB为斜边作等腰直角△ABD（点D在线段AB的上方）
①直线m过点（0，b）且与x轴平行，若直线m上存在△ABD的等距离点，试画图说明b的取值范围；
②已知点M（5，3），N（5+，3），若线段MN上的所有点均为△ABD的等距离点，请直接写出t的取值范围．（提示：若等腰直角三角形的腰长为1，则斜边长为2．）2组卷：88引用：3难度：0.1
