点P为平面内任意一点，若△ABC上存在点Q，满足PQ=1，则称点P为△ABC的等距离点．在平面直角坐标系xOy中，点A（t-4，1）与点B关于过点（t,0）且垂直于x轴的直线对称．
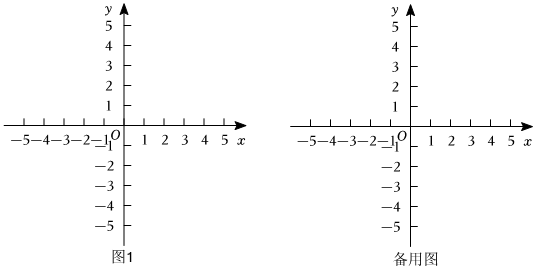
（1）以AB为底边作等腰△ABC，
①t=0，点B的坐标为 （4，1）（4，1）；
②当t=1，且底边AB上的高为3时，点C的坐标为 （1，4）或（1，-2）（1，4）或（1，-2）．
（2）以AB为斜边作等腰直角△ABD（点D在线段AB的上方）
①直线m过点（0，b）且与x轴平行，若直线m上存在△ABD的等距离点，试画图说明b的取值范围；
②已知点M（5，3），N（5+2，3），若线段MN上的所有点均为△ABD的等距离点，请直接写出t的取值范围．（提示：若等腰直角三角形的腰长为1，则斜边长为2．）
2
2
【考点】三角形综合题．
【答案】（4，1）；（1，4）或（1，-2）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/25 4:0:1组卷：88引用：3难度：0.1
相似题
-
1．如图，在△ABC中，∠ACB=90°，AB=10cm,BC=6cm,若点P从点A出发，以每秒4cm的速度沿折线A→C→B→A运动，设运动时间为t秒（0＜t＜6）．
（1）若点P在AC上，且满足△BCP的周长为14cm,则t的值为 ；
（2）若点P在∠BAC的平分线上，求此时t的值；
（3）运动过程中，直接写出当t为何值时，△BCP为等腰三角形．发布：2025/5/24 9:30:2组卷：140引用：4难度：0.3 -
2．在△ABC中，AB≠AC，点O为BC边的中点，连接AO，将△AOC绕点O顺时针方向旋转（旋转角为钝角），得到△EOF，连接AE，CF．
（1）如图1，当∠BAC=90°时，请直接写出AE与CF的数量关系 ．
（2）如图2，延长AO到点D，使OD=OA，连接DE，若AO=CF=5，BC=6．
①求的值；AECF
②求DE的长．
发布：2025/5/24 9:30:2组卷：187引用：1难度：0.3 -
3．如图1，△ABC中，∠ACB=90°，AC=BC，点D，E分别在边AC，AB上，且DE∥BC．
（1）则的值为 ；CDBE
（2）将△ADE绕点A逆时针旋转到如图2的位置，旋转角为α（45°＜α＜90°），连接CD，BE，求的值；CDBE
（3）将△ADE绕点A旋转，当∠DEB=90°，AC=5，AD=时，请直接写出线段CD的长．5
发布：2025/5/24 9:30:2组卷：324引用：3难度：0.2
