2022-2023学年福建省厦门市双十中学高三（上）月考数学试卷（10月份）

一、选择题：本大题共8小题，每小题5分，共40分．在每小题所给出的四个备选项中，只有一项是符合题目要求的．

• 1．设全集U={x∈Z|-3＜x＜4}，集合A={-2，0，1，2}，B={-1，0，1}，则A∩（∁_UB）=（　　）

  A．{-2，2}

  B．{-1，3}

  C．{-2，2，3}

  D．{-1}
  组卷：221引用：3难度：0.8

  解析

• 2．若命题“∀x∈R，x²+ax+1≥0”是假命题，则实数a的取值范围为（　　）

  A．（-∞，-2）∪（2，+∞）	B．（-∞，-2]
  C．[2，+∞）	D．（-∞，-2]∪[2，+∞）
  组卷：1599引用：6难度：0.7

  解析

• 3．已知

  a

  =

  （

  1

  2

  ）

  -

  0

  .

  6

  ，

  b

  =

  lo

  g

  1

  2

  2

  9

  ，

  c

  =

  4

  1

  3

  ，则a,b,c的大小关系是（　　）

  A．c＜b＜a

  B．b＜a＜c

  C．a＜c＜b

  D．b＜c＜a
  组卷：1014引用：12难度：0.8

  解析

• 4．已知直线l₁：（a-2）x+ay+2=0，l₂：x+（a-2）y+a=0，则“l₁⊥l₂”是“a=-1”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：292引用：7难度：0.8

  解析

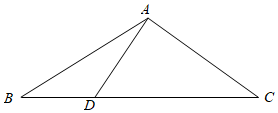• 5．如图，在△ABC中，∠BAC=120°，AB=2，AC=1，D是边BC上一点，DC=2BD，则

  AD

  •

  BC

  =（　　）

  A． 2 3

  B． - 7 4

  C． 5 2

  D． - 8 3
  组卷：464引用：10难度：0.7

  解析

• 6．已知三棱维A-BCD中，侧面ABC⊥底面BCD，△ABC是边长为6的正三角形，△BCD是直角三角形，且

  ∠

  BCD

  =

  π

  2

  ，

  CD

  =

  4

  ，则此三棱锥外接球的表面积为（　　）

  A．36π

  B．48π

  C．64π

  D．128π
  组卷：685引用：4难度：0.5

  解析

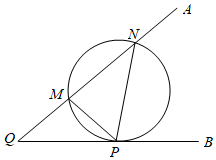• 7．几何学史上有一个著名的米勒问题：“设点M，N是锐角∠AQB的一边QA上的两点，试在QB边上找一点P，使得∠MPN最大”．如图，其结论是：点P为过M，N两点且和射线QB相切的圆的切点．根据以上结论解决以下问题：在平面直角坐标系xOy中，给定两点M（-1，2），N（1，4），点P在x轴上移动，当∠MPN取最大值时，点P的横坐标是（　　）

  A．-7

  B．1或-7

  C．2或-7

  D．1
  组卷：343引用：12难度：0.5

  解析

四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．已知椭圆

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的离心率为

  1

  2

  ，右焦点为F，两焦点与短轴两端点围成的四边形面积为

  2

  3

  ．
  （Ⅰ）求椭圆C的标准方程；
  （Ⅱ）直线l与椭圆有唯一的公共点M（M在第一象限），此直线l与y轴的正半轴交于点N，直线NF与直线OM交于点P且

  S

  △

  OFP

  =

  3

  7

  S

  △

  OFN

  ，求直线l的斜率．
  组卷：648引用：6难度：0.5

  解析

• 22．已知函数f（x）=（2e-x）lnx,其中e=2.71828…为自然对数的底数．
  （1）讨论函数f（x）的单调性；
  （2）若x₁，x₂∈（0，1），且x₂lnx₁-x₁lnx₂=2ex₁x₂（lnx₁-lnx₂），证明：

  2

  e

  ＜

  1

  x

  1

  +

  1

  x

  2

  ＜

  2

  e

  +

  1

  ．
  组卷：533引用：3难度：0.1

  解析