当前位置：试卷中心 > 试卷详情

2023年河南省创新发展联盟高考数学模拟预测试卷（文科）

发布：2024/6/14 8:0:9

一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知集合
A
=
{
x
|
y
=
1
-
x
}
，则∁_RA=（　　）
A．{x|x≤0} B．{x|x≤1} C．{x|x＞0} D．{x|x＞1}
组卷：193引用：1难度：0.9
解析
2．复数z=i（1-i）+2在复平面内对应的点位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：110引用：3难度：0.8
解析
3．在等比数列{a_n}中，若a₅=2，a₃a₈=a₇，则{a_n}的公比q=（　　）
A．
2
B．2 C．
2
2
D．4
组卷：887引用：7难度：0.8
解析
4．已知某班共有学生46人，该班语文老师为了了解学生每天阅读课外书籍的时长情况，决定利用随机数表法从全班学生中抽取10人进行调查．将46名学生按01，02，…，46进行编号．现提供随机数表的第7行至第9行：
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 57 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
若从表中第7行第41列开始向右依次读取2个数据，每行结束后，下一行依然向右读数，则得到的第8个样本编号是（　　）
A．07 B．12 C．39 D．44
组卷：401引用：8难度：0.9
解析
5．已知函数f（x）是定义在R上的奇函数，且f（x-3）=f（x）+1，则f（6）=（　　）
A．-1 B．1 C．-2 D．2
组卷：448引用：1难度：0.7
解析
6．已知函数f（x）=e^x-1-lnx-a,若对任意的x∈[1，+∞），f（x）≥0成立，则a的最大值是（　　）
A．ln2 B．
1
e
C．1 D．e
组卷：207引用：5难度：0.5
解析
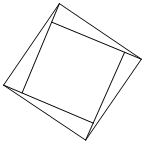7．勾股定理，在我国又称为“商高定理”，最早的证明是由东汉末期数学家赵爽在为《周髀算经》作注时给出的，他利用了勾股圆方图，此图被称为“赵爽弦图”．“赵爽弦图”是由四个全等的直角三角形和中间的一个小正方形组成的大正方形图案（如图所示），若在大正方形内随机取一点，该点落在小正方形内的概率为
9
17
，则“赵爽弦图”里的直角三角形中最小角的正弦值为（　　）
A．
2
17
B．
34
34
C．
2
17
.. D．
17
17
组卷：38引用：4难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

（二）选考题：共10分.请考生从第22，23两题中任选一题作答.如果多做，则按所做的第一个题目计分.[选修4-4：坐标系与参数方程]

22．在平面直角坐标系xOy中，曲线C的参数方程为
x
=
2
+
4
cosα
，
y
=
4
sinα
（α为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程是ρcosθ-ρsinθ-3=0．
（1）求曲线C的直角坐标方程和直线l的普通方程；
（2）若P（0，-3），直线l与曲线C交于A，B两点，M是线段AB的中点，求
|
PM
|
|
PA
|
+
|
PB
|
的值．
组卷：189引用：9难度：0.6
解析