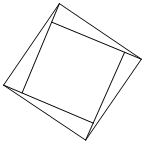
勾股定理，在我国又称为“商高定理”，最早的证明是由东汉末期数学家赵爽在为《周髀算经》作注时给出的，他利用了勾股圆方图，此图被称为“赵爽弦图”．“赵爽弦图”是由四个全等的直角三角形和中间的一个小正方形组成的大正方形图案（如图所示），若在大正方形内随机取一点，该点落在小正方形内的概率为917，则“赵爽弦图”里的直角三角形中最小角的正弦值为（ ）
9
17
【考点】几何概型．
【答案】D
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/14 8:0:9组卷：39引用：4难度：0.6
相似题
-
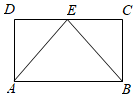1．如图，矩形ABCD中，点E为边CD的中点，若在矩形ABCD内部随机取一个点Q，则点Q取自△ABE内部的概率等于．发布：2025/1/13 8:0:2组卷：30引用：12难度：0.7 -
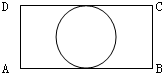2．如图所示，在矩形ABCD中，AB=4cm,BC=2cm,在图形上随机撒一粒黄豆，则黄豆落到圆上的概率是．发布：2025/1/13 8:0:2组卷：9引用：2难度：0.7 -
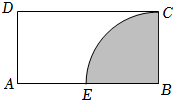3．如图，矩形ABCD，AB=2，BC=1，阴影部分为B为圆心，BC为半径的圆与矩形的重合部分，现在向矩形内随机投掷一点，则该点落在阴影部分以外的概率为（ ）发布：2024/12/29 15:30:4组卷：1引用：1难度：0.7
