2023年广东省佛山市禅城区高考数学模拟试卷（二）

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={x|x²-2x-3＜0}，B={x|1≤x≤5}，则A∪B=（　　）

  A．[1，3）

  B．（-1，1]

  C．（1，3）

  D．（-1，5]
  组卷：282引用：2难度：0.9

  解析

• 2．已知角α的终边与单位圆的交点为

  P

  （

  x

  ,

  3

  2

  ）

  ，则cos2α=（　　）

  A． 1 2

  B． - 1 2

  C． - 3 2

  D． 3 2
  组卷：284引用：3难度：0.8

  解析

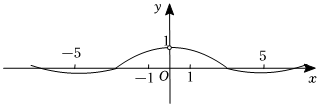• 3．已知函数y=f（x）的部分图象如图所示，则该函数的解析式，可能为（　　）

  A． f （ x ） = sinx x	B． f （ x ） = e x - e - x x
  C．f（x）=|sinx|cosx	D． f （ x ） = ln （ x 2 + 1 - x ） + sinx
  组卷：202引用：5难度：0.7

  解析

• 4．已知a,b为两条直线，α，β为两个平面，且满足a⊂α，b⊂β，α∩β=l,a∥l,则“a与b异面”是“直线b与l相交”的（　　）

  A．充分而不必要条件	B．必要而不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：690引用：9难度：0.6

  解析

• 5．已知圆C：（x-1）²+y²=4，过点A（0，1）的两条直线l₁，l₂互相垂直，圆心C到直线l₁，l₂的距离分别为d₁，d₂，则d₁d₂的最大值为（　　）

  A． 2 2

  B．1

  C． 2

  D．4
  组卷：293引用：2难度：0.5

  解析

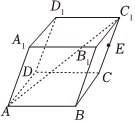• 6．如图，在平行六面体ABCD-A₁B₁C₁D₁中，以顶点A为端点的三条棱长都是a,且AB⊥AD，∠A₁AB=∠A₁AD=60°，E为CC₁的中点，则点E到直线AC₁的距离为（　　）

  A． 5 10 a

  B． 5 5 a

  C． 5 4 a

  D． 5 3 a
  组卷：167引用：5难度：0.5

  解析

• 7．现随机安排甲、乙等4位同学参加校运会跳高、跳远、投铅球比赛，要求每位同学参加一项比赛，每项比赛至少一位同学参加，事件A=“甲参加跳高比赛”，事件B=“乙参加跳高比赛”，事件C=“乙参加跳远比赛”，则（　　）

  A．事件A与B相互独立	B．事件A与C为互斥事件
  C． P （ C | A ） = 5 12	D． P （ B | A ） = 1 9
  组卷：546引用：22难度：0.5

  解析

四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.

• 21．在平面直角坐标系中，点O为坐标原点，M（-1，0），N（1，0），Q为线段MN上异于M，N的一动点，点P满足

  |

  PM

  |

  |

  QM

  |

  =

  |

  PN

  |

  |

  QN

  |

  =2．
  （1）求点P的轨迹E的方程；
  （2）点A，C是曲线E上两点，且在x轴上方，满足AM∥NC，求四边形AMNC面积的最大值．
  组卷：77引用：3难度：0.5

  解析

• 22．已知函数f（x）=x（a-e^2x），其中a∈R．
  （1）讨论函数f（x）极值点的个数；
  （2）对任意的x＞0，都有f（x）≤-lnx-1，求实数a的取值范围．
  组卷：131引用：3难度：0.2

  解析