2023-2024学年浙江省杭州市拱墅区文晖实验学校九年级（上）开学数学试卷

一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．

• 1．抛物线y=-2（x-2）²-5的顶点坐标是（　　）

  A．（-2，5）

  B．（2，5）

  C．（-2，-5）

  D．（2，-5）
  组卷：2823引用：31难度：0.9

  解析

• 2．抛物线y=x²-2是由抛物线y=x²（　　）

  A．向下平移2个单位长度得到

  B．向上平移2个单位长度得到

  C．向左平移2个单位长度得到

  D．向右平移2个单位长度得到
  组卷：36引用：5难度：0.9

  解析

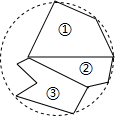• 3．小明不慎把家里的圆形镜子打碎了，其中三块碎片如图所示，三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是（　　）

  A．①

  B．②

  C．③

  D．均不可能
  组卷：3793引用：30难度：0.7

  解析

• 4．对于二次函数y=x²-4x-1的图象，下列说法错误的是（　　）

  A．开口向上

  B．与x轴有两个交点

  C．抛物线的对称轴为直线x=2

  D．当x≥2时，y随x的增大而减小
  组卷：563引用：3难度：0.6

  解析

• 5．函数

  y

  =

  （

  m

  -

  3

  ）

  x

  m

  2

  -

  7

  +2020x-2020是关于x的二次函数，则m的值为（　　）

  A．3

  B．0

  C．-3

  D．±3
  组卷：1169引用：16难度：0.7

  解析

• 6．在Rt△ABC中，∠ACB=90°，AC=6，AB=10，以C为圆心，BC为半径作⊙C，则点A与⊙C的位置关系是（　　）

  A．点A在⊙C内

  B．点A在⊙C上

  C．点A在⊙C外

  D．无法确定
  组卷：1193引用：19难度：0.9

  解析

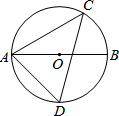• 7．如图，AB是⊙O的直径，点C、D在圆周上，∠CAB=30°，则∠ADC的度数为（　　）

  A．30°

  B．45°

  C．60°

  D．75°
  组卷：552引用：6难度：0.6

  解析

三、解答题（本大题共7小题，共66分.解答时应写出文字说明、证明过程或演算步骤）

• 22．根据以下素材，探索完成任务．
  

  如何设计喷灌器喷水口的升降方案
  素材1	随着自动化设备的普及，家庭庭院也引入自动喷灌系统．图1中某庭院内有一个可垂直升降的草坪喷灌器，从喷水口喷出的水柱成抛物线形．图2是该喷灌器OA喷水时的截面示意图，喷水口A点离地高度为0.25m,喷出的水柱在离喷水口水平距离为2m处达到最高，高度为0.45m,且水柱刚好落在庭院围墙和地面的交界B点处．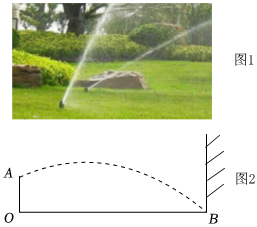
  素材2	为了美化庭院，准备在庭院内沿围墙建花坛种植绣球花，花坛高0.4m,宽0.8m,侧面用大理石包围，长方形BCDE是花坛截面，如图3．调整喷水口的高度，喷出的水柱形状与原来相同，水柱落在花坛的上方DE边上（大理石厚度不计），达到给花坛喷灌的效果．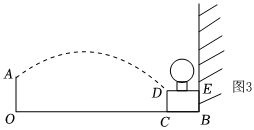
  问题解决
  任务1	确定水柱的形状	在图2中，建立合适的平面直角坐标系，求抛物线的表达式．
  任务2	确定喷灌器的位置	求出喷灌器OA与围墙的距．
  任务3	拟定喷头升降方案	调整喷水口的高度，使水柱可以喷灌花坛，求喷水口距离地面高度的最小值．
  组卷：840引用：3难度：0.4

  解析

• 23．若凸四边形的两条对角线所夹锐角为60°，我们称这样的凸四边形为“美丽四边形”．
  
  （1）①在“平行四边形、矩形、菱形、正方形”中，一定不是“美丽四边形”的有

  ；
  ②若矩形ABCD是“美丽四边形”，且AB=1，则BC=

  ；
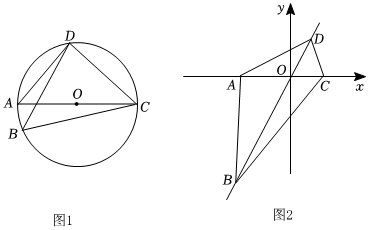
  （2）如图1，“美丽四边形”ABCD内接于⊙O，AC与BD相交于点P，且对角线AC，为直径，AP=2，PC=8，求另一条对角线BD的长；
  （3）如图2，平面直角坐标系中，已知“美丽四边形”ABCD的四个顶点A（-2，0），C（1，0），B在第三象限，D在第一象限，AC与BD交于点O，且四边形ABCD的面积为6

  3

  ，若二次函数y=ax²+bx+c（a、b、c为常数，且a≠0）的图象同时经过这四个顶点，求a的值．
  组卷：630引用：2难度：0.2

  解析