2023-2024学年贵州省贵阳市高三（上）摸底数学试卷（8月份）

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合是目要求的．

• 1．已知全集U=R，集合A={x|-1≤x≤3}，B={y|y=2^x，x∈R}，则下图阴影部分所对应的集合为（　　）

  A．{x|x＜-1}

  B．{x|x≤-1}

  C．{x|x≤0或x＞3}

  D．{x|0＜x≤3}
  组卷：119引用：3难度：0.8

  解析

• 2．已知（1+i）z=1（i为虚数单位），则|z|=（　　）

  A．1

  B． 2

  C．2

  D． 2 2
  组卷：13引用：2难度：0.8

  解析

• 3．2023年5月，浙江卫视《奔跑吧11》第四期节目打卡爽爽的贵阳城．包括周深在内的兄弟团成员和以刘宇等为成员的INTO1组合与来自贵阳社会各界的400位青年一起在贵州大学体育馆唱响了一场“青春歌会”．节目组在前期准备工作中统计出了排名靠前的10首人们喜欢的赞颂青春的歌曲．在活动中，兄弟团成员要从这10首歌曲中竞猜排名前5名的歌曲，则在竞猜中恰好猜对2首歌曲的概率为（　　）

  A． 32 63

  B． 25 63

  C． 5 126

  D． 1 252
  组卷：33引用：3难度：0.8

  解析

• 4．已知等差数列{a_n}的前n项和为S_n．若S₁=3，

  S

  2

  2

  +

  S

  4

  4

  =

  18

  ，则S₅=（　　）

  A．21

  B．48

  C．75

  D．83
  组卷：299引用：4难度：0.7

  解析

• 5．如图所示，△ABC中，点D是线段BC的中点，E是线段AD的靠近A的三等分点，则

  BE

  =（　　）

  A． - 5 6 AB + 1 6 AC

  B． - 2 3 AB + 1 3 AC

  C． - 5 6 AC + 1 6 AB

  D． - 2 3 AC + 1 3 AB
  组卷：1007引用：10难度：0.8

  解析

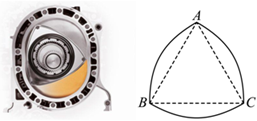• 6．转子发动机采用三角转子旋转运动来控制压缩和排放．如图，三角转子的外形是有三条侧棱的曲面棱柱，且侧棱垂直于底面，底面是以正三角形的三个顶点为圆心，正三角形的边长为半径画圆构成的曲面三角形，正三角形的顶点称为曲面三角形的顶点，侧棱长为曲面棱柱的高，记该曲面棱柱的底面积为S，高为h,已知曲面棱柱的体积V=Sh,若

  AB

  =

  6

  ，h=1，则曲面棱柱的体积为（　　）

  A． 3 π - 3 3

  B． 2 π - 2 2

  C． 3 π - 2 2

  D． 2 π - 3 3
  组卷：214引用：5难度：0.7

  解析

• 7．直线l经过抛物线y²=6x的焦点F，且与抛物线交于A，B两点．若|AF|=3|BF|，则|AB|=（　　）

  A．4

  B． 9 2

  C．8

  D． 9 4
  组卷：200引用：2难度：0.5

  解析

四、解答题：共6个小题，满分70分，解答应写出文字说明，证明过程或演算步骤．

• 21．在直角坐标平面内，已知A（-2，0），B（2，0），动点P满足条件：直线PA与直线PB斜率之积等于

  -

  1

  2

  ，记动点P的轨迹为E．
  （1）求E的方程；
  （2）过直线l：x=4上任意一点Q作直线QA与QB，分别交E于M，N两点，则直线MN是否过定点？若是，求出该点坐标；若不是，说明理由．
  组卷：128引用：4难度：0.5

  解析

• 22．牛顿迭代法是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法．比如，我们可以先猜想某个方程f（x）=0的其中一个根r在x=x₀的附近，如图所示，然后在点（x₀，f（x₀））处作f（x）的切线，切线与x轴交点的横坐标就是x₁，用x₁代替x₀重复上面的过程得到x₂；一直继续下去，得到x₀，x₁，x₂，…，x_n．从图形上我们可以看到x₁较x₀接近r,x₂较x₁接近r,等等．显然，它们会越来越逼近r.于是，求r近似解的过程转化为求x_n，若设精度为ε，则把首次满足|x_n-x_n-1|＜ε的x_n称为r的近似解．
  已知函数f（x）=x³+（a-2）x+a,a∈R．
  （1）当a=1时，试用牛顿迭代法求方程f（x）=0满足精度ε=0.5的近似解（取x₀=-1，且结果保留小数点后第二位）；
  （2）若f（x）-x³+x²lnx≥0，求a的取值范围．
  组卷：63引用：4难度：0.4

  解析