2022-2023学年浙江省高中联盟高二（上）期中数学试卷

一、选择题（本题共8小题，每小题5分，共40分．小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分）

• 1．设集合A={x|x（x-5）＜0}，B={x|0＜x＜1}，则A∩（∁_RB）等于（　　）

  A．{x|1＜x≤5}

  B．{x|x≥1}

  C．{x|x＜5}

  D．{x|1≤x＜5}
  组卷：47引用：3难度：0.8

  解析

• 2．若a,b∈R，则“复数z=a+bi为纯虚数（i是虚数单位）”是“b≠0”的（　　）

  A．充要条件	B．充分不必要条件
  C．必要不充分条件	D．既不充分也不必要条件
  组卷：98引用：5难度：0.8

  解析

• 3．向量

  a

  ，

  b

  分别是直线l₁，l₂的方向向量，且

  a

  =

  （

  1

  ，

  3

  ，

  5

  ）

  ，

  b

  =

  （

  x

  ,

  y

  ,

  2

  ）

  ，若l₁∥l₂，则

  a

  •

  b

  =（　　）

  A．12

  B．14

  C．16

  D．18
  组卷：118引用：6难度：0.7

  解析

• 4．已知定义域为R的奇函数f（x），满足f（1+x）=f（1-x），且当x∈[0，1]时，f（x）=2^x-1，则f（7）的值为（　　）

  A．-1

  B．0

  C．1

  D．2
  组卷：117引用：3难度：0.7

  解析

• 5．若圆锥的表面积为3π，其侧面展开图为一个半圆，则下列结论正确的为（　　）

  A．圆锥的母线长为2	B．圆锥的底面半径为2
  C．圆锥的体积为 3 3 π	D．圆锥的侧面积为π
  组卷：122引用：5难度：0.7

  解析

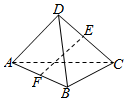• 6．三棱锥D-ABC中，AC=BD，且AC⊥BD，E，F分别分别是棱DC，AB的中点，则EF和AC所成的角等于（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：295引用：19难度：0.9

  解析

• 7．已知a=lg2，b=2^-1.5，

  c

  =

  sin

  2023

  π

  8

  ，则（　　）

  A．c＞b＞a

  B．b＞a＞c

  C．a＞b＞c

  D．c＞a＞b
  组卷：115引用：3难度：0.5

  解析

四、解答题（本题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤）

• 21．在①b（sinB+sinC+cosC）+ccosC=0，②sin（A+2B）+cos2B-sinA=1这两个条件中任选一个，补充在下面的横线上，并加以解答．
  已知△ABC的内角A，B，C的所对的边分别为a,b,c,____．
  （1）若

  B

  =

  π

  6

  ，求A；
  （2）求cosA+cosB+cosC的最大值．
  组卷：141引用：4难度：0.5

  解析

• 22．已知点P在圆O：x²+y²=6上运动，过点P作x轴的垂线段PQ，Q为垂足，动点M满足

  PQ

  =

  3

  MQ

  ．
  （1）求动点M的轨迹方程E；
  （2）过点（0，1）的动直线l与曲线E交于A，B两点，与圆O交于C，D两点，
  （i）求|AB|•|CD|的最大值；
  （ii）是否存在定点T，使得

  TA

  •

  TB

  的值是定值？若存在，求出点T的坐标及该定值；若不存在，请说明理由．
  组卷：109引用：3难度：0.6

  解析