2023-2024学年山西省太原三十六中九年级（上）月考数学试卷（10月份）
发布：2024/9/7 4:0:8
一、选择题（本大题共10小题，每小题3分，共30分。在每小题的四个选项中，只有一项最符合题意，请选出并在答题卡上将该项涂黑。）
-
1．下列方程中，属于一元二次方程的是（ ）
组卷：2001引用：38难度：0.8 -
2．一元二次方程x2-8x-1=0配方后可变形为（ ）
组卷：1345引用：251难度：0.7 -
3．方程x2=5x的解是（ ）
组卷：731引用：12难度：0.7 -
4．用求根公式解一元二次方程3x2-2=4x时a,b,c的值是（ ）
组卷：796引用：5难度：0.7 -
5．如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，AB=8，则CD的长为（ ）组卷：286引用：3难度：0.6 -
6．如图，两张等宽的纸条交叉叠放在一起，重合部分构成四边形ABCD．测得A，B的距离为6，A，C的距离为4，则B，D的距离是（ ）组卷：710引用：4难度：0.5 -
7．电影《满江红》于2023年1月22日在中国大陆上映，某地第一天票房约2亿元，以后每天票房按相同的增长率增长，三天后票房收入累计达7亿元，若把增长率记作x,则方程可以列为（ ）
组卷：355引用：8难度：0.6
三、解答题（本大题共8小题，75分。解答题应写出文字说明、证明过程或演算步骤。）
-
22．小明在学习矩形这一节时知道“直角三角形斜边上的中线等于斜边的一半”，由此引发他的思考，这个定理的逆命题成立吗？猜想：“如果一个三角形一边上的中线等于这条边的一半，那么这个三角形为直角三角形”．
通过探究，小明发现这个猜想也成立，以下是小明的证明过程：
已知：如图1，在△ABC中，D是AB边的中点，连接CD，且CD=AB．12
求证：△ABC为直角三角形．
证明：由条件可知，AD=BD=CD，则∠A=∠DCA，∠B=∠DCB．
又∵∠A+∠DCA+∠B+∠DCB=180°，
∴∠DCA+∠DCB=∠ACB=90°，即△ABC为直角三角形．
爱动脑筋的小明发现用本学期所学知识也能证明这个结论，并想出了图2，图3两种不同的证明思路，请你选择其中一种，把证明过程补充完整：证法一：如图2，延长CD至点E，使DE=CD，连接AE，BE． 证法二：如图3，分别取AC，BC边的中点E，F，连接DE，DF，EF，则DE，DF，EF为△ABC的中位线． 组卷：205引用：2难度：0.6 -
23．探究问题：
（1）方法感悟：
如图1，在正方形ABCD中，点E、F分别为DC、BC边上的点，且满足∠EAF=45°，连接EF，求证：DE+BF=EF．
感悟解题方法，并完成下列填空：
将△ADE绕点A顺时针旋转90°得到△ABG，此时AD与AB重合，由旋转可得：
AB=AD，BG=DE，∠1=∠2，∠ABG=∠D=90°，
∴∠ABG+∠ABF=90°+90°=180°，
因此，点G、B、F在同一条直线上．
∵∠EAF=45°，
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°．
∵∠1=∠2，∴∠1+∠3=45°．
即∠GAF=∠．
又 AG=AE，AF=AF，∴△GAF≌．
∴=EF，故DE+BF=EF；
（2）方法迁移：
如图2，将Rt△ABC沿斜边翻折得到△ADC，点E、F分别为DC、BC边上的点，且∠EAF=∠DAB．试猜想DE、BF、EF之间有何数量关系，并证明你的猜想；12
（3）问题拓展：
如图3，在四边形ABCD中，AB=AD，E、F分别为DC、BC上的点，满足∠EAF=∠DAB，试猜想当∠B与∠D满足什么关系时，可使得DE+BF=EF．请直接写出你的猜想（不必说明理由）．12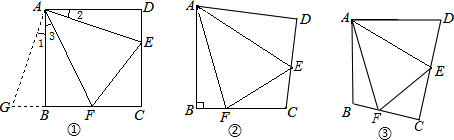
组卷：504引用：7难度：0.1
