当前位置：试卷中心 > 试卷详情

2022-2023学年湖南省岳阳市岳阳县一中高一（下）期末数学试卷

发布：2024/6/10 8:0:9

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知
a
、
b
和
c
均为非零向量，
①若
a
•
（
b
•
c
）
=
（
a
•
b
）
•
c
，则
a
∥
c
；②若
a
•
c
=
b
•
c
，则
a
=
b
；③若
|
（
a
•
b
）
•
c
|
=
|
a
|
|
b
|
|
c
|
，则
a
∥
b
．
上述命题中，真命题的个数是（　　）
A．0 B．1 C．2 D．3
组卷：112引用：5难度：0.6
解析
2．在△ABC中，
BE
=
1
2
EC
，D是AC的中点，若
AC
=
x
AE
+
y
BD
，则
x
y
=（　　）
A．
1
2
B．2 C．
3
2
D．3
组卷：79引用：4难度：0.7
解析
3．若z=
1
-
i
1
+
i
+4-2i,则|z|=（　　）
A．5 B．4 C．3 D．2
组卷：163引用：5难度：0.8
解析
4．某学校在校学生有3000人，为了增强学生的体质，学校举行了跑步和登山比赛，每人都参加且只参加其中一项比赛，高一、高二、高三年级参加跑步的人数分别为a,b,c,且a：b：c=2：3：4，全校参加登山的人数占总人数的
2
5
．为了了解学生对本次比赛的满意程度，按分层抽样的方法从中抽取一个容量为300的样本进行调查，则应从高二年级参加跑步的学生中抽取（　　）
A．15人 B．30人 C．45人 D．60人
组卷：170引用：6难度：0.8
解析
5．O为▱ABCD两条对角线的交点，
AB
=4
e
1
，
BC
=6
e
2
，则
DO
=（　　）
A．2
e
1
+
e
2
B．2
e
1
-
e
2
C．2
e
1
+3
e
2
D．2
e
1
-3
e
2
组卷：83引用：6难度：0.8
解析
6．已知α，β，γ是三个不同的平面，m,n是两条不同的直线，则下列命题中正确的是（　　）
A．若α⊥γ，β⊥γ，则α∥β B．若m∥α，m∥β，则α∥β
C．若m⊥α，n⊥α，则m∥n D．若m∥α，n∥α，则m∥n
组卷：76引用：8难度：0.6
解析
7．函数
f
（
x
）
=
lnx
-
1
x
的零点为x₀，且x₀∈[k,k+1），k∈Z，则k的值为（　　）
A．1 B．2 C．0 D．3
组卷：187引用：5难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

21．已知函数
f
（
x
）
=
lo
g
2
（
x
-
1
-
a
+
1
）
的定义域为[1，+∞）．
（1）求
y
=
7
+
a
-
4
1
-
a
的最大值；
（2）若a＞0，求
y
=
1
2
a
（
3
-
2
a
）
的最大值．
组卷：67引用：4难度：0.6
解析
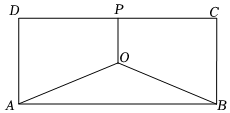22．某地有四家工厂，分别位于矩形ABCD的四个顶点．已知AB=20km,BC=10km.为了处理这四家工厂的污水，当地政府打算在该矩形区域上（含边界）建造一个污水处理厂O，并铺设一些管道连通各家工厂和污水处理厂．记需要铺设管道的总长度为L（单位：km）．现有以下两种建设方案．
（1）第一种方案计划将污水处理厂建在矩形区域内部，并在各家工厂与污水处理厂之间用管道直接连通．求该方案下L的最小值；
（2）第二种方案计划将污水处理厂O建在对角线AC、BD的交点处，并在矩形区域内部选择两个关于O对称的点P、Q作为管道的分叉点，如图所示．试确定该方案下L取得最小值时，分叉点P、Q的位置．
组卷：25引用：4难度：0.4
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．若α⊥γ，β⊥γ，则α∥β	B．若m∥α，m∥β，则α∥β
C．若m⊥α，n⊥α，则m∥n	D．若m∥α，n∥α，则m∥n

2022-2023学年湖南省岳阳市岳阳县一中高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知a、b和c均为非零向量，①若a•（b•c）=（a•b）•c，则a∥c；②若a•c=b•c，则a=b；③若|（a•b）•c|=|a||b||c|，则a∥b．上述命题中，真命题的个数是（ ）

2．在△ABC中，BE=12EC，D是AC的中点，若AC=xAE+yBD，则xy=（ ）

3．若z=1-i1+i+4-2i,则|z|=（ ）

5．O为▱ABCD两条对角线的交点，AB=4e1，BC=6e2，则DO=（ ）

6．已知α，β，γ是三个不同的平面，m,n是两条不同的直线，则下列命题中正确的是（ ）

7．函数f（x）=lnx-1x的零点为x0，且x0∈[k,k+1），k∈Z，则k的值为（ ）

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

21．已知函数f（x）=log2（x-1-a+1）的定义域为[1，+∞）．（1）求y=7+a-41-a的最大值；（2）若a＞0，求y=12a（3-2a）的最大值．

1．已知
a
、
b
和
c
均为非零向量，
①若
a
•
（
b
•
c
）
=
（
a
•
b
）
•
c
，则
a
∥
c
；②若
a
•
c
=
b
•
c
，则
a
=
b
；③若
|
（
a
•
b
）
•
c
|
=
|
a
|
|
b
|
|
c
|
，则
a
∥
b
．
上述命题中，真命题的个数是（　　）

2．在△ABC中，
BE
=
1
2
EC
，D是AC的中点，若
AC
=
x
AE
+
y
BD
，则
x
y
=（　　）

3．若z=
1
-
i
1
+
i
+4-2i,则|z|=（　　）

5．O为▱ABCD两条对角线的交点，
AB
=4
e
1
，
BC
=6
e
2
，则
DO
=（　　）

6．已知α，β，γ是三个不同的平面，m,n是两条不同的直线，则下列命题中正确的是（　　）

7．函数
f
（
x
）
=
lnx
-
1
x
的零点为x₀，且x₀∈[k,k+1），k∈Z，则k的值为（　　）

21．已知函数
f
（
x
）
=
lo
g
2
（
x
-
1
-
a
+
1
）
的定义域为[1，+∞）．
（1）求
y
=
7
+
a
-
4
1
-
a
的最大值；
（2）若a＞0，求
y
=
1
2
a
（
3
-
2
a
）
的最大值．