2023年广东省广州113中中考数学三模试卷

一、选择题（本大题共10小题，共30分）

• 1．要使

  x

  -

  1

  在实数范围内有意义，则x的取值范围是（　　）

  A．x≤1

  B．x＞1

  C．x≥0

  D．x≥1
  组卷：485引用：12难度：0.9

  解析

• 2．已知点A（2-a,a+1）在第一象限，则a的取值范围是（　　）

  A．a＞2

  B．-1＜a＜2

  C．-2＜a＜-1

  D．a＜1
  组卷：552引用：5难度：0.7

  解析

• 3．下列运算中，正确的是（　　）

  A．x3•x3=x6	B．（x2）3=x5
  C．3x2÷2x=x	D．（x-y）2=x2-y2
  组卷：182引用：8难度：0.7

  解析

• 4．下列说法中，正确的是（　　）

  A．为了解长沙市中学生的睡眠情况实行全面调查

  B．一组数据-1，2，5，5，7，7，4的众数是7

  C．明天的降水概率为90%，则明天下雨是必然事件

  D．若平均数相同的甲、乙两组数据，s甲2=0.3，s乙2=0.02，则乙组数据更稳定
  组卷：215引用：8难度：0.7

  解析

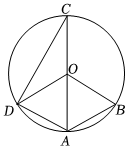• 5．如图，AC是⊙O的直径，点B、D在⊙O上，

  AB

  =

  AD

  =

  3

  ，∠AOB=60°，则CD的长度是（　　）

  A． 6

  B． 2 3

  C．3

  D．6
  组卷：498引用：7难度：0.6

  解析

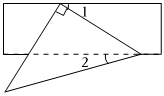• 6．将等腰直角三角形纸片和长方形纸片按如图方式叠放，若∠1=25°，则∠2的度数为（　　）

  A．45°

  B．30°

  C．25°

  D．20°
  组卷：189引用：7难度：0.7

  解析

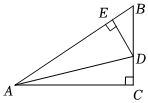• 7．如图，在Rt△ABC中，∠C=90°，点D和点E分别是BC和AB上的点，已知DE⊥AB，

  sin

  B

  =

  4

  5

  ，AC=8，CD=2，则DE的长为（　　）

  A．3.2

  B．4

  C．4.5

  D．4.8
  组卷：576引用：8难度：0.7

  解析

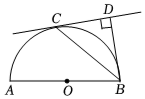• 8．已知，如图，点C是以AB为直径的半圆O上一点，过点C作⊙O的切线CD，BD⊥CD于点D，若∠DCB=50°，则∠ABC的度数是（　　）

  A．25°

  B．40°

  C．45°

  D．50°
  组卷：376引用：4难度：0.5

  解析

三、解答题（本大题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤）

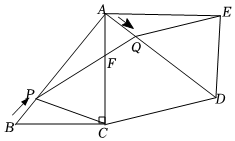• 24．如图，在Rt△ABC中，∠ACB=90°，AB=5cm,BC=3cm,将△ABC绕点A按逆时针方向旋转90°得到△ADE，连接CD．点P从点B出发，沿BA方向匀速运动、速度为1cm/s；同时，点Q从点A出发，沿AD方向匀速运动，速度为1cm/s.PQ交AC于点F，连接CP，EQ，设运动时间为t（s）（0＜t＜5）．解答下列问题：
  （1）当EQ⊥AD时，求t的值；
  （2）设四边形PCDQ的面积为S（cm²），求S与t之间的函数关系式；
  （3）是否存在某一时刻t,使PQ∥CD？若存在，求出t的值；若不存在，请说明理由．
  组卷：2377引用：7难度：0.2

  解析

• 25．已知抛物线y=x²+tx-t-1（t＞0）过点（h,-4），交x轴于A，B两点（点A在点B左侧），交y轴于点C，且对于任意实数m,恒有m²+tm-t-1≥-4成立．
  （1）求抛物线的解析式；
  （2）在抛物线的对称轴上，是否存在点M，使得∠BMC=∠BAC，若存在，求出点M的坐标，若不存在，请说明理由；
  （3）若P₁（n-2，y₁），P₂（n,y₂），P₃（n+2，y₃）三点都在抛物线上且总有y₃＞y₁＞y₂，请直接写出n的取值范围．
  组卷：453引用：3难度：0.3

  解析