2023-2024学年重庆市万州第二高级中学高二（上）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的4个选项中，只有一项是符合题目要求的．

• 1．直线y=tan45°的斜率为（　　）

  A．1

  B．0

  C．-1

  D．不存在
  组卷：31引用：2难度：0.8

  解析

• 2．若向量

  a

  =（2，0，-1），向量

  b

  =（0，1，-2），则2

  a

  -

  b

  =（　　）

  A．（-4，1，-4）

  B．（-4，1，0）

  C．（4，-1，0）

  D．（4，-1，-4）
  组卷：1872引用：21难度：0.9

  解析

• 3．平面内点P到F₁（-3，0）、F₂（3，0）的距离之和是10，则动点P的轨迹方程是（　　）

  A． x 2 25 + y 2 9 = 1	B． x 2 25 + y 2 16 = 1
  C． y 2 25 + x 2 9 = 1	D． y 2 25 + x 2 16 = 1
  组卷：86引用：19难度：0.7

  解析

• 4．点A（6，0），P在直线y=-x上，

  |

  AP

  |

  =

  3

  2

  ，则P点的个数是（　　）

  A．0

  B．1

  C．2

  D．3
  组卷：40引用：3难度：0.8

  解析

• 5．已知

  v

  为直线l的方向向量，

  n

  1

  ，

  n

  2

  分别为平面α，β的法向量（α，β不重合）那么下列说法中：
  ①

  n

  1

  ∥

  n

  2

  ⇔α∥β；②

  n

  1

  ⊥

  n

  2

  ⇔α⊥β；③

  v

  ∥

  n

  1

  ⇔l∥α；④

  v

  ⊥

  n

  1

  ⇔l⊥α．正确的有（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：189引用：10难度：0.8

  解析

• 6．直线l：mx-y+1-2m=0与圆C：（x-2）²+（y-4）²=10相交所形成的长度为整数的弦的条数为（　　）

  A．6

  B．7

  C．8

  D．9
  组卷：45引用：1难度：0.6

  解析

• 7．若直线l：kx-y+3k=0与曲线

  C

  ：

  1

  -

  x

  2

  =

  y

  -

  1

  有两个不同的交点，则实数k的取值范围是（　　）

  A． （ 1 2 ， 3 4 ]

  B． [ 1 2 ， 3 4 ）

  C． （ 0 ， 3 4 ）

  D． （ 0 ， 3 4 ]
  组卷：1625引用：18难度：0.5

  解析

四、解答题：本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤．

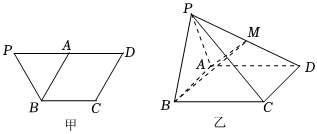• 21．如图甲，在四边形PBCD中，PD∥BC，PB=BC=CD=AD=PA=2，将△ABP沿AB折起得图乙，点M是PD上的点．
  （1）若M为PD的中点，证明：PC⊥平面ABM；
  （2）若PC=

  6

  ，试确定M的位置，使二面角M-AB-C的正弦值等于

  2

  5

  5

  ．
  组卷：184引用：3难度：0.5

  解析

• 22．已知椭圆K：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）的左、右焦点分别为F₁（-2，0），F₂（2，0），过右焦点F₂的直线l交椭圆K于M，N两点，以线段|MF₂|为直径的圆C与圆C₁：x²+y²=8内切．
  （1）求椭圆K的方程；
  （2）过点M作ME⊥x轴于点E，过点N作NQ⊥x轴于点Q，OM与NE交于点P，是否存在直线l截得△PMN的面积等于

  6

  2

  ？若存在，求出直线l的方程；若不存在，请说明理由．
  组卷：186引用：2难度：0.5

  解析