当前位置：试卷中心 > 试卷详情

2022-2023学年湖南省长沙市雅礼中学高三（下）月考数学试卷（八）

发布：2024/7/14 8:0:9

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A={x∈Z|x²-4x-12＜0}，B={y|y=esinx,x∈R}，则A∩B=（　　）
A．{-2，-1，0，1，2} B．{x|-1＜x＜2}
C．{-1，0，1，2} D．{x|x≥2，x≤-1}
组卷：13引用：2难度：0.8
解析

2．下列说法正确的是（　　）

A．“a≥b”是“am²≥bm²”的充要条件

B．“

kπ

，

∈

”是“tanx=1”的必要不充分条件

C．命题“

∃

∈

，

≥

”的否定形式是“

∀

∈

，

＞

”

D．“xy=1”是“lgx+lgy=0”的充分不必要条件

组卷：195引用：5难度：0.7

解析

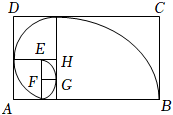3．斐波那契螺旋线被誉为自然界最完美的“黄金螺旋”，它的画法是：以斐波那契数1，1，2，3，5，8，…为边长比例的正方形拼成矩形，然后在每个正方形中画一个圆心角为90°的圆弧，这些圆弧所连起来的弧线就是斐波那契螺旋线．如图，矩形ABCD是由若干符合上述特点的正方形拼接而成，其中|AB|=16，则图中的斐波那契螺旋线的长度为（　　）
A．11π B．12π C．15π D．16π
组卷：146引用：7难度：0.8
解析
4．在平面直角坐标系中，已知点P（3，4）为角α终边上一点，若cos（α+β）=
1
3
，β∈（0，π），则cosβ=（　　）
A．
3
-
8
2
15
B．
3
+
8
2
15
C．
4
+
6
2
15
D．
6
2
-
4
15
组卷：420引用：6难度：0.7
解析
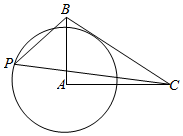5．已知直角三角形ABC中，∠A=90°，AB=2，AC=4，点P在以A为圆心且与边BC相切的圆上，则
PB
•
PC
的最大值为（　　）
A．
16
+
16
5
5
B．
16
+
8
5
5
C．
16
5
D．
56
5
组卷：1003引用：12难度：0.5
解析
6．已知a=0.75，b=2log₅2，
c
=
sin
π
5
，则a,b,c的大小关系是（　　）
A．c＜b＜a B．b＜c＜a C．c＜a＜b D．a＜c＜b
组卷：462引用：4难度：0.7
解析
7．若函数
f
（
x
）
=
e
x
x
3
-
a
（
3
x
+
lnx
）
只有一个极值点，则a的取值范围是（　　）
A．
（
-
∞
，
e
2
4
]
B．（-∞，0]
C．
（
-
∞
，
0
]
∪
{
e
3
9
}
D．
（
-
∞
，
e
2
4
]
∪
{
e
3
9
}
组卷：129引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分。请在答题卡指定区域内作答。解答时应写出文字说明、证明过程或演算步骤。

21．已知椭圆具有如下光学性质：从椭圆的一个焦点发出的光线射向椭圆上任一点，经椭圆反射后必经过另一个焦点．若从椭圆
T
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左焦点F₁发出的光线，经过两次反射之后回到点F₁，光线经过的路程为8，T的离心率为
3
2
．
（1）求椭圆T的标准方程；
（2）设D（x_D，0），且x_D＞a,过点D的直线l与椭圆T交于不同的两点M，N，F₂是T的右焦点，且∠DF₂M与∠DF₂N互补，求△MNF₂面积的最大值．
组卷：88引用：2难度：0.4
解析
22．已知函数
f
（
x
）
=
e
x
-
1
6
a
x
3
（a为非零常数），记f_n+1（x）=f'_n（x）（n∈N），f₀（x）=f（x）．
（1）当x＞0时，f（x）≥0恒成立，求实数a的最大值；
（2）当a=1时，设
g
n
（
x
）
=
n
∑
i
=
2
f
i
（
x
）
，对任意的n≥3，当x=t_n时，y=g_n（x）取得最小值，证明：g_n（t_n）＞0且所有点（t_n，g_n（t_n））在一条定直线上．
组卷：75引用：5难度：0.3
解析