当前位置：试卷中心 > 试卷详情

2023-2024学年辽宁省大连市金州高级中学高一（上）月考数学试卷（10月份）

发布：2024/9/8 12:0:8

一、单选题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1．已知U={x∈N|x≤7}，A={0，1，2}，B={1，2，3}，则∁_U（A∩B）=（　　）
A．{3，4，5，6，7} B．{0，4，5，6，7}
C．{0，3，4，5，6，7} D．{0，3，5，6，7}
组卷：108引用：3难度：0.8
解析
2．命题“∀x∈R，x²-2x+12≤0”的否定为（　　）
A．∃x₀∈R，x₀²-2x₀+12＞0 B．∀x∈R，x²-2x+12≥0
C．∀x∉R，x²-2x+12≤0 D．∃x₀∉R，x₀²-2x₀+12＞0
组卷：221引用：8难度：0.8
解析
3．已知集合
A
=
{
α
|
α
=
π
3
+
kπ
，
k
∈
Z
}
，
B
=
{
β
|
β
=
2
π
3
+
kπ
3
，
k
∈
Z
}
，下列描述正确的是（　　）
A．A∩B=A B．A∩B=B
C．A∩B=∅ D．以上选项都不对
组卷：66引用：3难度：0.7
解析
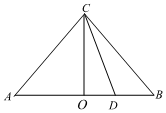4．数学里有一种证明方法叫做Proofswithoutwords,也称之为无字证明，一般是指仅用图象语言而无需文字解释就能不证自明的数学命题，由于这种证明方法的特殊性，无字证明被认为比严格的数学证明更为优雅．现有如图所示图形，在等腰直角三角形ABC中，点O为斜边AB的中点，点D为斜边AB上异于顶点的一个动点，设AD=a,BD=b,则该图形可以完成的无字证明为（　　）
A．
a
+
b
2
≥
ab
（
a
＞
0
，
b
＞
0
）
B．
a
+
b
2
≤
a
2
+
b
2
2
（
a
＞
0
，
b
＞
0
）
C．
2
ab
a
+
b
≤
ab
（
a
＞
0
，
b
＞
0
）
D．
a
2
+
b
2
≥
2
ab
（
a
＞
0
，
b
＞
0
）
组卷：557引用：8难度：0.5
解析
5．不等式ax²+bx+c≥0的解集为{x|-1≤x≤2}，则关于x的不等式cx²-bx+a＜0的解集为（　　）
A．（-2，1） B．
（
1
2
，
1
）
C．（-2，-1） D．
（
-
1
2
，
1
）
组卷：49引用：1难度：0.7
解析
6．已知x₁，x₂是关于x的方程x²-2mx+m²+2m+3=0的两个实数根．则
x
2
1
+
x
2
2
的最小值（　　）
A．-6 B．-8 C．
9
2
D．
3
2
组卷：79引用：2难度：0.7
解析
7．不等式mx²+2mx-4＜2x²+4x解集为R，则实数m的取值范围是（　　）
A．（-2，2] B．（-2，2）
C．（-∞，-2）∪[2，+∞） D．（-∞，-2）
组卷：527引用：37难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本题共6小题，共70分，其中第17题10分，其它每题12分，解答应写出文字说明、证明过程或演算步㵵）

21．已知关于的不等式（k²-2k-3）x²+（k+1）x+1＞0（k∈R）的解集为M．
（1）若存在两个不相等负实数a、b,使得M=（-∞，a）∪（b,+∞），求实数k的取值范围；
（2）是否存在实数k,满足：“对于任意n∈N^*，都有n∈M，对于任意的m∈Z^-，都有m∉M”，若存在，求出k的值，若不存在，说明理由．
组卷：16引用：1难度：0.6
解析
22．已知二次函数y=ax²+bx+c.
（1）若对任意x∈R，b=2，a＞c且不等式y≥0恒成立，并且存在x₀∈R，使得
ax
2
0
+2x₀+c=0成立，求
a
2
+
c
2
a
-
c
的最小值．
（2）若对任意x∈R，若a＜b且不等式y≥0恒成立，求
a
+
2
b
+
4
c
b
-
a
的最小值．
组卷：29引用：1难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．{3，4，5，6，7}	B．{0，4，5，6，7}
C．{0，3，4，5，6，7}	D．{0，3，5，6，7}

A．∃x₀∈R，x₀²-2x₀+12＞0	B．∀x∈R，x²-2x+12≥0
C．∀x∉R，x²-2x+12≤0	D．∃x₀∉R，x₀²-2x₀+12＞0

A．A∩B=A	B．A∩B=B
C．A∩B=∅	D．以上选项都不对

A． a + b 2 ≥ ab （ a ＞ 0 ， b ＞ 0 ）	B． a + b 2 ≤ a 2 + b 2 2 （ a ＞ 0 ， b ＞ 0 ）
C． 2 ab a + b ≤ ab （ a ＞ 0 ， b ＞ 0 ）	D． a 2 + b 2 ≥ 2 ab （ a ＞ 0 ， b ＞ 0 ）

A．（-2，2]	B．（-2，2）
C．（-∞，-2）∪[2，+∞）	D．（-∞，-2）

2023-2024学年辽宁省大连市金州高级中学高一（上）月考数学试卷（10月份）

一、单选题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1．已知U={x∈N|x≤7}，A={0，1，2}，B={1，2，3}，则∁U（A∩B）=（ ）

2．命题“∀x∈R，x2-2x+12≤0”的否定为（ ）

3．已知集合A={α|α=π3+kπ，k∈Z}，B={β|β=2π3+kπ3，k∈Z}，下列描述正确的是（ ）

5．不等式ax2+bx+c≥0的解集为{x|-1≤x≤2}，则关于x的不等式cx2-bx+a＜0的解集为（ ）

6．已知x1，x2是关于x的方程x2-2mx+m2+2m+3=0的两个实数根．则x21+x22的最小值（ ）

7．不等式mx2+2mx-4＜2x2+4x解集为R，则实数m的取值范围是（ ）

四、解答题（本题共6小题，共70分，其中第17题10分，其它每题12分，解答应写出文字说明、证明过程或演算步㵵）

22．已知二次函数y=ax2+bx+c.（1）若对任意x∈R，b=2，a＞c且不等式y≥0恒成立，并且存在x0∈R，使得ax20+2x0+c=0成立，求a2+c2a-c的最小值．（2）若对任意x∈R，若a＜b且不等式y≥0恒成立，求a+2b+4cb-a的最小值．

1．已知U={x∈N|x≤7}，A={0，1，2}，B={1，2，3}，则∁_U（A∩B）=（　　）

2．命题“∀x∈R，x²-2x+12≤0”的否定为（　　）

3．已知集合
A
=
{
α
|
α
=
π
3
+
kπ
，
k
∈
Z
}
，
B
=
{
β
|
β
=
2
π
3
+
kπ
3
，
k
∈
Z
}
，下列描述正确的是（　　）

5．不等式ax²+bx+c≥0的解集为{x|-1≤x≤2}，则关于x的不等式cx²-bx+a＜0的解集为（　　）

6．已知x₁，x₂是关于x的方程x²-2mx+m²+2m+3=0的两个实数根．则
x
2
1
+
x
2
2
的最小值（　　）

7．不等式mx²+2mx-4＜2x²+4x解集为R，则实数m的取值范围是（　　）

22．已知二次函数y=ax²+bx+c.
（1）若对任意x∈R，b=2，a＞c且不等式y≥0恒成立，并且存在x₀∈R，使得
ax
2
0
+2x₀+c=0成立，求
a
2
+
c
2
a
-
c
的最小值．
（2）若对任意x∈R，若a＜b且不等式y≥0恒成立，求
a
+
2
b
+
4
c
b
-
a
的最小值．