2022-2023学年广东省深圳实验学校高中部高一（下）期中数学试卷

一、单选题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知向量

  a

  =（1，2），

  b

  =（-1，m），若

  a

  ⊥

  b

  ，则m的值为（　　）

  A．-2

  B．2

  C． 1 2

  D． - 1 2
  组卷：213引用：8难度：0.9

  解析

• 2．复数

  z

  =

  （

  1

  +

  3

  i

  ）

  3

  （

  2

  +

  2

  i

  ）

  2

  +

  3

  +

  i

  2

  -

  i

  ，则

  z

  的虚部是（　　）

  A．2

  B．2i

  C．i

  D．-2
  组卷：123引用：1难度：0.7

  解析

• 3．已知单位向量

  a

  ，

  b

  满足|

  a

  -

  b

  |=

  3

  ，则cos＜

  a

  ，

  a

  +

  b

  ＞=（　　）

  A． - 1 2

  B． 1 2

  C． 3 2

  D． - 3 2
  组卷：254引用：4难度：0.8

  解析

• 4．从正方体的8个顶点上任取4个顶点，则这4个顶点构成的几何图形不可能是（　　）

  A．三个面是直角三角形的正三棱锥

  B．有一个面是钝角三角形的四面体

  C．每个面都是等边三角形的四面体

  D．每个面都是直角三角形的四面体
  组卷：134引用：1难度：0.5

  解析

• 5．在△ABC中，已知cos2A+cos2B-cos2C=1-2sinAsinB，则一定成立的是（　　）

  A． A = π 3

  B． A = π 4

  C．A=C

  D． C = π 3
  组卷：175引用：1难度：0.7

  解析

• 6．在△ABC中，

  a

  =

  x

  ,

  b

  =

  3

  ，

  B

  =

  60

  °

  ，若三角形有两解，则x的取值范围是（　　）

  A． 2 ＜ x ＜ 2 2

  B． 2 ＜ x ＜ 2

  C． 3 ＜ x ＜ 2

  D． 2 ＜ x ＜ 2 3
  组卷：235引用：1难度：0.7

  解析

• 7．过△ABC的重心G的直线l分别交线段AB、AC于点E、F，若

  AE

  =

  λ

  AB

  ，

  AF

  =

  μ

  AC

  ，则2λ+μ的最小值为（　　）

  A． 1 + 2 2 3

  B． 3 + 2 2

  C． 2 + 2 2 3

  D． 5 3
  组卷：229引用：1难度：0.6

  解析

四、解答题：共70分．解答应写出文字说明、证明过程或演算步骤

• 21．正六棱台玻璃容器的两底面棱长分别为7cm,31cm,高为32cm,如图水平放置，盛有水深为12cm.
  （1）求玻璃容器的体积；
  （2）将一根长度为40cm的搅棒l置入玻璃容器中，l的一端置于点E处，另一端置于侧棱GG₁上，求l没入水中部分的长度．（容器厚度，搅棒粗细均忽略不计）
  组卷：117引用：4难度：0.5

  解析

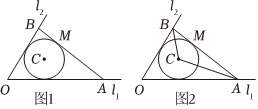• 22．如图1，某景区是一个以C为圆心，半径为

  3

  km

  的圆形区域，道路l₁，l₂成60°角，且均和景区边界相切，现要修一条与景区相切的观光木栈道AB，点A，B分别在l₁和l₂上，修建的木栈道AB与道路l₁，l₂围成三角地块OAB．（注：圆的切线长性质：圆外一点引圆的两条切线长相等）．
  （1）若△OAB的面积

  S

  =

  10

  3

  k

  m

  2

  ，求木栈道AB长；
  （2）如图2，若景区中心C与木栈道A段连线的∠CAB=α，求木栈道AB的最小值．
  组卷：59引用：2难度：0.5

  解析