当前位置：试卷中心 > 试卷详情

2023-2024学年山东省济南一中高二（上）月考数学试卷（10月份）

发布：2024/9/10 18:0:8

一、单选题

1．已知直线过点（1，2），且纵截距为横截距的两倍，则直线l的方程为（　　）
A．2x-y=0 B．2x+y-4=0
C．2x-y=0或x+2y-2=0 D．2x-y=0或2x+y-4=0
组卷：965引用：28难度：0.8
解析
2．过点（-2，0）与圆x²+y²-4x-m=0相切的两条直线垂直，则m=（　　）
A．-4 B．
-
2
2
C．
2
2
D．4
组卷：487引用：7难度：0.7
解析
3．如果方程x²+ky²=2表示焦点在y轴上的椭圆，那么实数k的取值范围是（　　）
A．（1，+∞） B．（1，2） C．（
1
2
，1） D．（0，1）
组卷：310引用：12难度：0.7
解析
4．阿波罗尼斯是古希腊著名数学家，与阿基米德、欧几里得并称为亚历山大时期数学三巨匠，他研究发现：如果一个动点P到两个定点的距离之比为常数λ（λ＞0，且λ≠1），那么点P的轨迹为圆，这就是著名的阿波罗尼斯圆．若点C到A（-1，0），B（1，0）的距离之比为
3
，则点C到直线x-2y+8=0的距离的最小值为（　　）
A．
2
5
-
3
B．
5
-
3
C．
2
5
D．
3
组卷：213引用：10难度：0.5
解析
5．设x,y∈R，向量
a
=（x,1，1），
b
=（1，y,1），
c
=（2，-4，2），且
a
⊥
c
，
b
∥
c
，则|
a
+
b
|=（　　）
A．
2
2
B．
10
C．3 D．4
组卷：2698引用：74难度：0.8
解析
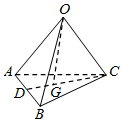6．如图，G是△ABC的重心，
OA
=
a
，
OB
=
b
，
OC
=
c
，则
OG
=（　　）
A．
1
3
a
+
2
3
b
+
2
3
c
B．
2
3
a
+
2
3
b
+
1
3
c
C．
2
3
a
+
2
3
b
+
2
3
c
D．
1
3
a
+
1
3
b
+
1
3
c
组卷：54引用：14难度：0.9
解析
7．已知两定点A（-3，5），B（2，8），动点P在直线x-y+1=0上，则|PA|+|PB|的最小值为（　　）
A．5
13
B．
34
C．5
5
D．
2
26
组卷：1726引用：12难度：0.7
解析
8．在下列四个命题中：
①若向量
a
，
b
所在的直线为异面直线，则向量
a
，
b
一定不共面；
②向量
a
=
（
2
，-
1
，
2
）
，
b
=
（
-
4
，
2
，
m
）
，若
a
与
b
的夹角为钝角，则实数m的取值范围为m＜5；
③直线
x
a
+
y
b
=
1
的一个方向向量为
（
1
，-
b
a
）
；
④若存在不全为0的实数x,y,z使得
x
a
+
y
b
+
z
c
=
0
，则
a
，
b
，
c
共面．
其中正确命题的个数是（　　）
A．0 B．1 C．2 D．3
组卷：202引用：5难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题

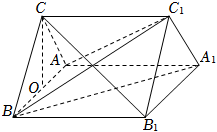23．如图，直三棱柱ABC-A₁B₁C₁中，ABC是边长为2的正三角形，O为AB的中点．
（1）证明：CO⊥平面ABB₁A₁；
（2）若直线B₁C与平面ABB₁A₁所成的角的正切值为
15
5
，求平面A₁BC₁与平面ABC₁夹角的余弦值．
组卷：125引用：8难度：0.4
解析
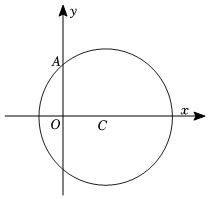24．已知圆C的圆心坐标为C（3，0），且该圆经过点A（0，4）．
（1）求圆C的标准方程；
（2）若点B也在圆C上，且弦AB长为8，求直线AB的方程；
（3）直线l交圆C于M，N两点，若直线AM，AN的斜率之积为2，求证：直线l过一个定点，并求出该定点坐标．
组卷：246引用：8难度：0.4
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．2x-y=0	B．2x+y-4=0
C．2x-y=0或x+2y-2=0	D．2x-y=0或2x+y-4=0

A． 1 3 a + 2 3 b + 2 3 c	B． 2 3 a + 2 3 b + 1 3 c
C． 2 3 a + 2 3 b + 2 3 c	D． 1 3 a + 1 3 b + 1 3 c

2023-2024学年山东省济南一中高二（上）月考数学试卷（10月份）

一、单选题

1．已知直线过点（1，2），且纵截距为横截距的两倍，则直线l的方程为（ ）

2．过点（-2，0）与圆x2+y2-4x-m=0相切的两条直线垂直，则m=（ ）

3．如果方程x2+ky2=2表示焦点在y轴上的椭圆，那么实数k的取值范围是（ ）

5．设x,y∈R，向量a=（x,1，1），b=（1，y,1），c=（2，-4，2），且a⊥c，b∥c，则|a+b|=（ ）

6．如图，G是△ABC的重心，OA=a，OB=b，OC=c，则OG=（ ）

7．已知两定点A（-3，5），B（2，8），动点P在直线x-y+1=0上，则|PA|+|PB|的最小值为（ ）

四、解答题

23．如图，直三棱柱ABC-A1B1C1中，ABC是边长为2的正三角形，O为AB的中点．（1）证明：CO⊥平面ABB1A1；（2）若直线B1C与平面ABB1A1所成的角的正切值为155，求平面A1BC1与平面ABC1夹角的余弦值．

1．已知直线过点（1，2），且纵截距为横截距的两倍，则直线l的方程为（　　）

2．过点（-2，0）与圆x²+y²-4x-m=0相切的两条直线垂直，则m=（　　）

3．如果方程x²+ky²=2表示焦点在y轴上的椭圆，那么实数k的取值范围是（　　）

5．设x,y∈R，向量
a
=（x,1，1），
b
=（1，y,1），
c
=（2，-4，2），且
a
⊥
c
，
b
∥
c
，则|
a
+
b
|=（　　）

6．如图，G是△ABC的重心，
OA
=
a
，
OB
=
b
，
OC
=
c
，则
OG
=（　　）

7．已知两定点A（-3，5），B（2，8），动点P在直线x-y+1=0上，则|PA|+|PB|的最小值为（　　）

23．如图，直三棱柱ABC-A₁B₁C₁中，ABC是边长为2的正三角形，O为AB的中点．
（1）证明：CO⊥平面ABB₁A₁；
（2）若直线B₁C与平面ABB₁A₁所成的角的正切值为
15
5
，求平面A₁BC₁与平面ABC₁夹角的余弦值．