2022-2023学年江苏省徐州市鼓楼区树人中学八年级（上）期中数学试卷
发布：2024/9/6 3:0:8
一、选择题（本大题共有8小题，每题3分，共2分。在每小题所给出的四个选项中，只有一项是符合题目要求的，请将正确选项的字母代号填写在答题卡相应的位置）
-
1．现实世界中，对称现象无处不在，中国的方块字有些也具有对称性下列汉字是轴对称图形的是（ ）
组卷：94引用：6难度：0.9 -
2．满足下列条件的△ABC，不是直角三角形的是（ ）
组卷：488引用：17难度：0.9 -
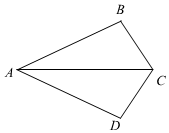3．如图，已知AB=AD，下列条件中，添加后仍不能判定△ABC≌△ADC的是（ ）组卷：610引用：12难度：0.8 -
4．等腰三角形的底角为50°，则这个等腰三角形的顶角为（ ）
组卷：462引用：9难度：0.9 -
5．如图，以△ABC的顶点A为圆心，BC的长为半径作弧；再以顶点C为圆心，AB的长为半径作弧，两弧交于点D；连接AD，CD，则△ABC≌△CDA，理由是（ ）组卷：184引用：4难度：0.6 -
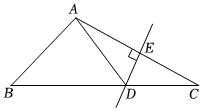6．如图，△ABC中，DE是AC的垂直平分线，AE=5cm,△ABD的周长为18cm,则△ABC的周长为（ ）组卷：1607引用：12难度：0.9 -
7．《九章算术》中记载：今有户不知高、广，竿不知长、短．横之不出四尺，从之不出二尺，斜之适出．问户高、广、斜各几何？
译文是：今有门，不知其高、宽，有竿，不知其长、短．横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线恰好相等．问门高、宽、对角线长分别是多少？若设门对角线长为x尺，则可列方程为（ ）组卷：1371引用：23难度：0.5 -
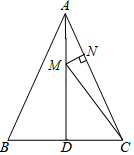8．如图，△ABC中，AB=AC=13，BC=10，AD是BC边上的中线，M是AD上的一个动点，作MN⊥AC交AC于N，则CM+MN的最小值为（ ）组卷：1371引用：3难度：0.5
三、解答题
-
24．工人师傅有一块不规则的模板，他已经在模板上画出了一条裁割线AB，现根据木板的情况，需要通过AB上一点C，作AB的垂线，进行裁割，但手头没有直角尺，怎么办呢？
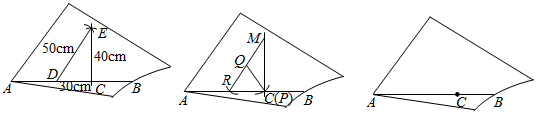
方法一：如图1，取卷尺在AB上量出CD=30cm,然而分别以D，C为圆心，以50cm与40cm为半径画圆弧，两弧相交于点E，作直线CE，则∠DCE=90°；
方法二：如图2，在绳子EF上割取任意长度a,一端记点P，另一端记为点Q，将P点与C点重合，按如图位置摆放，然后以Q为圆心，PQ的长为半径画弧，交AB于点R，连接RQ，并延长到点M使得QM=QR，连接CM，则∠MCR=90°．
任务：（1）方法一依据的数学原理是 ．
（2）利用方法2，证明∠MCR=90°；
（3）方法三，尺规作图：如图3，请在木板上，过点C作出AB的垂线l（保留作图痕迹，不写作法）．组卷：81引用：1难度：0.5 -
25．同学们，等边三角形、等腰直角三角形都是最常见的几何图形．
（1）如图1，以等边△ABC的边BC为腰作等腰直角△BCD，其中∠DBC=90°，BD=CB，点D，点A都在BC同侧，延长BD、CA交于点M、连接AD，求∠MAD的度数．
（2）如图2，在（1）的条件下，作BN平分∠DBC交AC于点N，求证：MD=CN；
（3）如图3，将图（1）的△CBD沿着BC翻折得到△CBD1，连接AD1，P为AD1中点，连接BP并延长交CD1于点Q、请猜测CQ、BP、PQ三条线段之间的数量关系，并证明你的结论．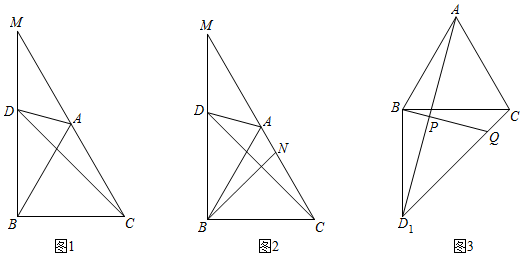
组卷：2053引用：9难度：0.2
