2022-2023学年山西省临汾市襄汾县八年级（下）期末数学试卷

一、选择题（本大题共10小题，每小题3分，共30分.在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑)

• 1．分式

  1

  3

  +

  x

  有意义的条件是（　　）

  A．x=-3

  B．x≠-3

  C．x≠3

  D．x≠0
  组卷：1166引用：14难度：0.7

  解析

• 2．在平面直角坐标系中，点A（2，-3）位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：2514引用：55难度：0.7

  解析

• 3．小明与小华本学期都参加了5次数学考试（总分均为100分），数学老师想判断这两位同学的数学成绩谁更稳定，在作统计分析时，老师需比较这两人5次数学成绩的（　　）

  A．平均数

  B．方差

  C．众数

  D．中位数
  组卷：119引用：4难度：0.7

  解析

• 4．在平行四边形ABCD中，∠A+∠C=210°，则∠B的度数为（　　）

  A．30°

  B．75°

  C．95°

  D．105°
  组卷：443引用：3难度：0.8

  解析

• 5．如果反比例函数y=

  a

  -

  2

  x

  （a是常数）的图象在第一、三象限，那么a的取值范围是（　　）

  A．a＜0

  B．a＞0

  C．a＜2

  D．a＞2
  组卷：2799引用：38难度：0.9

  解析

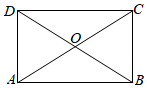• 6．如图，在平行四边形ABCD中，对角线AC、BD相交于点O．下列条件不能判定平行四边形ABCD为矩形的是（　　）

  A．∠ABC=90°

  B．AC=BD

  C．AD=AB

  D．∠BAD=∠ADC
  组卷：1085引用：11难度：0.5

  解析

• 7．下列语句正确的是（　　）

  A．对角线互相垂直的四边形是菱形

  B．有两对邻角互补的四边形为平行四边形

  C．矩形的对角线相等

  D．平行四边形是轴对称图形
  组卷：2108引用：22难度：0.9

  解析

三、解答题（本大题共8个小题，共75分.解答应写出文字说明，证明过程或演算步骤）

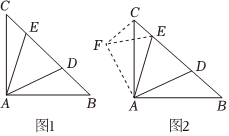• 22．阅读材料，解决问题
  折叠、旋转是我们常见的两种图形变化方式如图1，在Rt△ABC中，∠BAC=90°，AB=AC，点D，E在边BC上，∠DAE=45°，若BD=3，CE=1，求DE的长．小明发现，如果将△ABD绕点A按逆时针方向旋转90°，得到△ACF，连接EF（如图2）．使条件集中在△FCE中，可求得FE（即DE）的长，具体想法为：先旋转△ABD得到△ACF，再结合已知条件，可证△AEF≌△AED，最后在△FCE中可求得FE的长，即ED的长．
  （1）请你写出△AEF与△AED等的证明过程．
  （2）求出DE的长．
  组卷：50引用：1难度：0.6

  解析

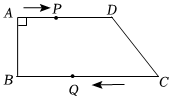• 23．如图，在四边形ABCD中，AD∥BC，∠A=90°，AB=8cm,AD=12cm,BC=18cm,点P从点A出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以2cm/s的速度向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设点P，Q运动的时间为t s.
  （1）CD边的长度为

  cm,t的取值范围为

  ．
  （2）从运动开始，当t=

  时，PQ=CD．
  （3）在整个运动过程中是否存在t值，使得四边形PQCD是菱形．若存在，请求出t值；若不存在，请说明理由．
  组卷：41引用：1难度：0.3

  解析