阅读材料，解决问题
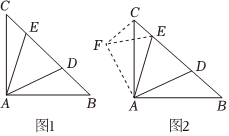
折叠、旋转是我们常见的两种图形变化方式如图1，在Rt△ABC中，∠BAC=90°，AB=AC，点D，E在边BC上，∠DAE=45°，若BD=3，CE=1，求DE的长．小明发现，如果将△ABD绕点A按逆时针方向旋转90°，得到△ACF，连接EF（如图2）．使条件集中在△FCE中，可求得FE（即DE）的长，具体想法为：先旋转△ABD得到△ACF，再结合已知条件，可证△AEF≌△AED，最后在△FCE中可求得FE的长，即ED的长．
（1）请你写出△AEF与△AED等的证明过程．
（2）求出DE的长．
【答案】（1）证明过程见解析；
（2）．
（2）
10
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/25 8:0:9组卷：50引用：1难度：0.6
相似题
-
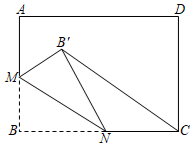1．如图，矩形ABCD中，AB=10，BC=12，M为AB中点，N为BC边上一动点，将△MNB沿MN折叠，得到△MNB'，则CB'的最小值为．发布：2025/5/25 18:30:1组卷：467引用：4难度：0.5 -
2．在矩形ABCD中，AB=4，AD=4
，以BC为直径作半圆（如图1），点P为边CD上一点．将矩形沿BP折叠，使得点C的对应点E恰好落在边AD上（如图2），则阴影部分周长是 ．2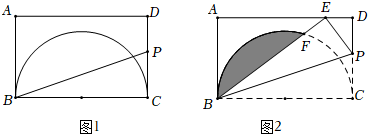
发布：2025/5/25 17:0:1组卷：53引用：3难度：0.5 -
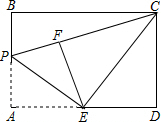3．如图，矩形ABCD中，AB=4，AD=6，点E为AD中点，点P为线段AB上一个动点，连接EP，将△APE沿PE折叠得到△FPE，连接CE，CF，当△ECF为直角三角形时，AP的长为．发布：2025/5/25 17:30:1组卷：1905引用：20难度：0.5
