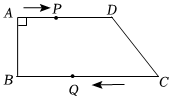
如图，在四边形ABCD中，AD∥BC，∠A=90°，AB=8cm,AD=12cm,BC=18cm,点P从点A出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以2cm/s的速度向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设点P，Q运动的时间为t s.
（1）CD边的长度为 1010cm,t的取值范围为 0≤t≤90≤t≤9．
（2）从运动开始，当t=4或84或8时，PQ=CD．
（3）在整个运动过程中是否存在t值，使得四边形PQCD是菱形．若存在，请求出t值；若不存在，请说明理由．
【考点】四边形综合题．
【答案】10；0≤t≤9；4或8
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/8 8:0:9组卷：42引用：1难度：0.3
相似题
-
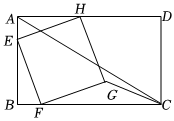1．如图，矩形ABCD中，AB=8，BC=12，正方形EFGH的三个顶点E，F，H分别在矩形ABCD的边AB、BC，DA上，点G在矩形内部，连接AC，CG，现给出以下结论：
①当AE=4时，S△FGC=16；
②当S△FGC=17.5时，AE=5；
③当A，G，C三点共线时，AG：GC=2：1；
④点G到CD的距离为定值．
其中正确的是 .（写出所有正确结论的序号）发布：2025/5/25 18:0:1组卷：333引用：2难度：0.4 -
2．【问题情境】数学课上，王老师出示了这样一个问题：如图1，在矩形ABCD中，AD=2AB，E是AB延长线上一点，且BE=AB，连接DE，交BC于点M，以DE为一边在DE的左下方作正方形DEFG，连接AM．试判断线段AM与DE的位置关系．
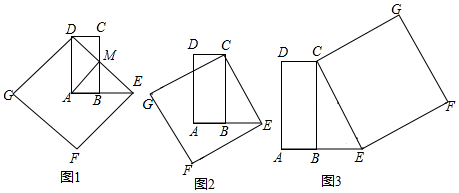
【探究展示】小明发现，AM垂直平分DE，并展示了如下的证明方法：
证明：∵BE=AB，∴AE=2AB．
∵AD=2AB，∴AD=AE．
∵四边形ABCD是矩形，
∴AD∥BC．
∴.（平行线分线段成比例）
∵BE=AB，
∴=1．EMDM
∴EM=DM．
即AM是△ADE的DE边上的中线，
又∵AD=AE，
∴.（等腰三角形的“三线合一”）
∴AM垂直平分DE．
【反思交流】
（1）请将上述证明过程补充完整；
（2）小颖受到小明的启发，继续进行探究，如图2，连接CE，以CE为一边在CE的左下方作正方形CEFG，发现点G在线段BC的垂直平分线上，请你给出证明；
【拓展应用】
（3）如图3，连接CE，以CE为一边在CE的右上方作正方形CEFG，分别以点B，C为圆心，m为半径作弧，两弧交于点M，连接MF．若MF=AB=1，请直接写出m的值．发布：2025/5/25 17:30:1组卷：266引用：2难度：0.3 -
3．问题提出
（1）如图1，在Rt△ABC中，∠ACB=90°．请在△ABC内画一个正方形，使得这个正方形一个内角为∠C，其余顶点落在△ABC的边上；
问题探究
（2）如图，△ABC为一块锐角三角形木板，其中BC=10，S△ABC=25．
如图2，若要在△ABC中做出一个正方形，使正方形边落在BC上，另外两个顶点分别落在AB，AC上，则该正方形的面积为 ．
如图3，若要在△ABC中做出一个平行四边形，使平行四边形一边EF落在BC上，另两顶点落在AB，AC上，请求出满足条件的平行四边形面积的最大值．
问题解决
（3）如图4有一四边形ABCD，AC与BD交于O，AC=10，BD=20，∠AOB=60°，现要在四边形ABCD中截出平行四边形EFGH，使得平行四边形一边EF与BD平行，四个顶点E，F，G，H落在ABCD的四边上，当S▱EFGH=S四边形ABCD时EF=．14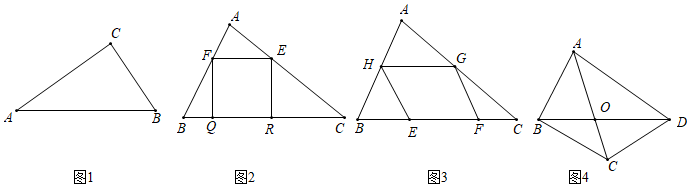
发布：2025/5/25 17:30:1组卷：358引用：3难度：0.1
