2022-2023学年海南省海口市海南中学高一（下）期末数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题所给出的四个选项中，只有一项是符合题目要求的.

• 1．已知i是虚数单位，复数z=（x²-4）+（x+2）i是纯虚数，则实数x的值为（　　）

  A．2

  B．-2

  C．±2

  D．4
  组卷：234引用：11难度：0.7

  解析

• 2．已知

  a

  =

  （

  3

  ，

  2

  ）

  ，

  b

  =

  （

  -

  6

  ，

  x

  ）

  ，若

  a

  与

  b

  共线，则x=（　　）

  A．-4

  B．4

  C．9

  D．-9
  组卷：309引用：6难度：0.8

  解析

• 3．过两直线l₁：x-3y+4=0和l₂：2x+y+5=0的交点和原点的直线方程为（　　）

  A．3x-19y=0

  B．19x-3y=0

  C．19x+3y=0

  D．3x+19y=0
  组卷：462引用：2难度：0.8

  解析

• 4．已知m,n是两条直线，α，β是两个平面，下列说法正确的是（　　）

  A．若m∥n,n∥α，则m∥α	B．若m∥n,n⊂α，则m∥α
  C．若m∥α，n⊂α，则m∥n	D．若m∥n,m⊥α，则n⊥α
  组卷：182引用：7难度：0.8

  解析

• 5．一个三角形的三条高的长度分别是

  1

  6

  ，

  1

  10

  ，

  1

  14

  ，则该三角形（　　）

  A．一定是锐角三角形

  B．一定是直角三角形

  C．一定是钝角三角形

  D．有可能是锐角三角形，也可能是钝角三角形
  组卷：34引用：4难度：0.8

  解析

• 6．已知正三棱台的上、下底面的棱长分别为3和6，侧棱长为2，则该正三棱台的体积为（　　）

  A． 19 3 2

  B． 21 3 2

  C． 19 3 4

  D． 21 3 4
  组卷：315引用：6难度：0.6

  解析

• 7．若

  {

  a

  ，

  b

  ，

  c

  }

  构成空间的一个基底，则下列向量能构成空间的一个基底的是（　　）

  A． b + c ， b ， b - c	B． a + b ， a - b ， c
  C． a ， a + b ， a - b	D． a + b ， a + b + c ， c
  组卷：335引用：6难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．如图，在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥CD．
  （1）求证：PD⊥AB；
  （2）若

  PA

  =

  QC

  ，设点E为线段PA上任意一点（不包含端点）．证明，直线CE与平面PQD相交．
  组卷：38引用：1难度：0.5

  解析

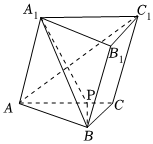• 22．已知三棱柱ABC-A₁B₁C₁中，AC=AA₁=4，BC=2，∠ACB=90°，A₁B⊥AC₁．
  （1）求证：平面A₁ACC₁⊥平面ABC；
  （2）若∠A₁AC=60°，在线段AC上是否存在一点P使平面BA₁P和平面A₁ACC₁所成角的正弦值为

  13

  4

  ？若存在，确定点P的位置、若不存在，说明理由．
  组卷：105引用：3难度：0.5

  解析