2022-2023学年广东省清远一中高一（上）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知命题p：∀x＞1，2x²-3=0，则命题p的否定是（　　）

  A．∃x＞1，2x2-3=0	B．∃x＞1，2x2-3≠0
  C．∀x＞1，2x2-3≠0	D．∀x≤1，2x2-3≠0
  组卷：10引用：2难度：0.8

  解析

• 2．已知集合M={x∈N^*|x≤2}，则以下关系正确的是（　　）

  A．0∈M

  B．2∉M

  C．{0，1，2}⊆M

  D．M⫋{0，1，2}
  组卷：17引用：3难度：0.9

  解析

• 3．函数

  f

  （

  x

  ）

  =

  x

  2

  -

  2

  x

  +

  1

  x

  -

  2

  的定义域是（　　）

  A．（0，2]	B．[2，+∞）
  C．（-∞，0]∪（2，+∞）	D．R
  组卷：22引用：4难度：0.9

  解析

• 4．已知幂函数f（x）的图象过点（2，8），则f（3）的值为（　　）

  A．3

  B．9

  C．27

  D． 1 3
  组卷：86引用：3难度：0.9

  解析

• 5．设函数

  f

  （

  x

  ）

  =

  x

  x

  +

  1

  ，则下列函数中为奇函数的是（　　）

  A．f（x+1）+1

  B．f（x-1）+1

  C．f（x+1）-1

  D．f（x-1）-1
  组卷：1273引用：4难度：0.8

  解析

• 6．已知a、b、c、d均为实数，则下列命题正确的是（　　）

  A．若a＜b,c＜d,则ac＜bd

  B．若ab＞0，bc-ad＞0，则 c a - d b ＜ 0

  C．若a＞b,c＞d,则a-d＞b-c

  D．若a＞b,c＞d＞0，则 a d ＞ b c
  组卷：65引用：2难度：0.8

  解析

• 7．已知某商品的进货成本为10（元/件），经过长时间调研，发现售价x（元）与月销售量y（件）满足函数关系式

  y

  =

  16000

  x

  2

  +

  800

  x

  ．为了获得最大利润，商品售价应为（　　）

  A．80元

  B．60元

  C．50元

  D．40元
  组卷：18引用：4难度：0.8

  解析

四、解答题：本大题共6小题，共70分.解答应写出必要的文字说明、证明过程及演算步骤.

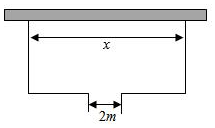• 21．如图，围建一个面积为360m²的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的一扇门，已知旧墙的维修费用为45元/m,新墙的造价为180元/m,一扇门的造价为600元，设利用的旧墙的长度为xm,总造价为y元．
  （1）将y表示为x的函数；
  （2）试确定x,使修建此矩形场地围墙的总费用最小，并求出最小总费用．
  组卷：171引用：4难度：0.5

  解析

• 22．已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）=-x²+2x.
  （1）求函数f（x）在R上的解析式；
  （2）若f（x）在[-2，b）上有最大值，求实数b的取值范围．
  组卷：265引用：6难度：0.8

  解析