2023-2024学年山东省多校高二(上)联合测评数学试卷(9月份)
发布:2024/8/16 14:0:1
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知
,则z的虚部是( )z=2+i1+i2+i5组卷:35引用:3难度:0.8 -
2.已知
,a是不共线的向量,且b,AB=a+2b,AC=2a+b,则( )CD=3a-3b组卷:345引用:5难度:0.9 -
3.天气预报说,在今后的三天中,每天下雨的概率都为60%.现采用随机模拟的方法估计这三天中恰有两天下雨的概率.用1,2,3,4,5,6表示下雨,用计算机产生了10组随机数为180,792,454,417,165,809,798,386,196,206.据此估计这三天中恰有两天下雨的概率近似为( )
组卷:279引用:13难度:0.8 -
4.若实数x,y满足2022x+2023-y<2022y+2023-x,则( )
组卷:111引用:2难度:0.7 -
5.若
,P(AB)=19,P(A)=23,则关于事件A与B的关系正确的是( )P(B)=13组卷:134引用:3难度:0.7 -
6.我国南北朝名著《张邱建算经》中记载:“今有方亭,下方三丈,上方一丈,高二丈五尺,预接筑为方锥,问:接筑高几何?”大致意思是:有一个正四棱台的上、下底面边长分别为一丈、三丈,高为二丈五尺,现从上面补上一段,使之成为正四棱锥,则所补的小四棱锥的高是多少?那么,此高和原四棱台的体积分别是( )(注:1丈等于10尺)
组卷:85引用:5难度:0.6 -
7.已知函数
在(0,f(x)=cos(ωx+π3)(ω>0))上仅有一个零点,则ω的取值范围是( )π2组卷:140引用:1难度:0.8
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.某市为了了解人们对“中国梦”的伟大构想的认知程度,针对该市不同年龄和不同职业的人举办了一次知识竞赛,满分100分(95分及以上为认知程度高),结果认知程度高的有m(m>20)人,按年龄分成5组,其中第一组:[20,25),第二组:[25,30),第三组:[30,35),第四组:[35,40),第五组:[40,45],得到如图所示的频率分布直方图.
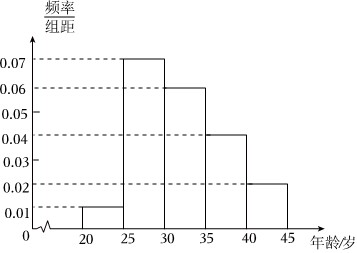
(1)根据频率分布直方图,估计这m人的平均年龄和80%分位数;
(2)现从以上各组中采用分层随机抽样的方法抽取20人,担任该市的宣传使者,若第四组宣传使者的年龄的平均数与方差分别为37和,第五组宣传使者的年龄的平均数与方差分别为43和1,估计这m人中35~45岁所有人的年龄的方差.52组卷:29引用:2难度:0.7 -
22.类比于二维平面中的余弦定理,有三维空间中的三面角余弦定理;
如图1,由射线PA,PB,PC构成的三面角P-ABC,∠APC=α,∠BPC=β,∠APB=γ,二面角A-PC-B的大小为θ,则cosγ=cosαcosβ+sinαsinβcosθ.
(1)当α、时,证明以上三面角余弦定理;β∈(0,π2)
(2)如图2,四棱柱ABCD-A1B1C1D1中,平面AA1C1C⊥平面ABCD,∠A1AC=60°,∠BAC=45°,
①求∠A1AB的余弦值;
②在直线CC1上是否存在点P,使BP∥平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.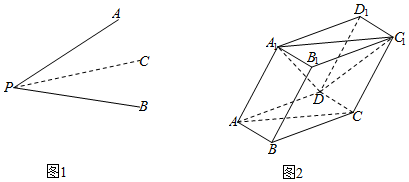 组卷:425引用:12难度:0.4
组卷:425引用:12难度:0.4


