2022-2023学年青海省海东市高一（下）期末数学试卷

一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符

• 1．已知集合A={x|1-x＞0}，B={x|x²＜9}，则A∪B=（　　）

  A．（-3，1）

  B．（-∞，1）

  C．（1，3）

  D．（-∞，3）
  组卷：123引用：5难度：0.7

  解析

• 2．某校有男生1800人，女生1600人，按照性别进行分层，采用分层随机抽样的方法从该校学生中抽取680人进行调查，则抽取的男生人数是（　　）

  A．320

  B．360

  C．380

  D．420
  组卷：45引用：1难度：0.8

  解析

• 3．函数

  y

  =

  5

  cos

  （

  2

  x

  +

  π

  4

  ）

  的图象向右平移

  π

  8

  个单位长度得到函数f（x）的图象，则

  f

  （

  π

  12

  ）

  =（　　）

  A． 5 2

  B．5

  C． 5 3 2

  D． 5 2 2
  组卷：71引用：3难度：0.7

  解析

• 4．已知a=log_0.30.2，b=0.3^0.2，c=log_0.91.2，则（　　）

  A．b＞a＞c

  B．b＞c＞a

  C．a＞c＞b

  D．a＞b＞c
  组卷：218引用：5难度：0.8

  解析

• 5．所有棱长均为6的正三棱锥被平行于其底面的平面所截，截去一个底面边长为2的正三棱锥，则所得棱台的高为（　　）

  A． 4 6 3

  B． 2 6 3

  C． 6

  D． 6 2
  组卷：131引用：3难度：0.7

  解析

• 6．柜子中有3双不同颜色的手套，红色、黑色、白色各1双．若从中随机地取出2只，则取出的手套是一只左手套一只右手套，但不是一双手套的概率为（　　）

  A． 1 5

  B． 2 5

  C． 3 5

  D． 4 5
  组卷：102引用：7难度：0.7

  解析

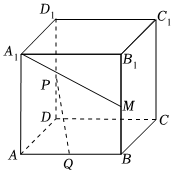• 7．如图，在正方体ABCD-A₁B₁C₁D₁中，P，Q，M分别是DD₁，AB，BB₁的中点，则异面直线A₁M与PQ所成角的余弦值为（　　）

  A． 15 5

  B． 30 10

  C． 5 6

  D． 2 5 3
  组卷：263引用：5难度：0.7

  解析

四、解答题：本大题共6小题，共70分，解答应写出必要的文字说明、证明过程或演算步骤.

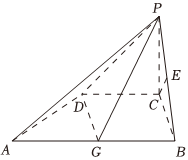• 21．如图，在四棱锥P-ABCD中，PC⊥平面ABCD，底面ABCD为等腰梯形，AB∥CD，∠DAB=60°，AB=2，CD=PC=1，E，G分别为BP，AB的中点．
  （1）证明：CE∥平面ADP；
  （2）从下面①②两个问题中任意选择一个解答，如果两个都解答，则按第一个计分，
  ①求点E到平面ADP的距离；
  ②求点E到平面PDG的距离．
  组卷：121引用：5难度：0.5

  解析

• 22．为了让羽毛球运动在世界范围内更好地发展，世界羽联将每年的7月5日定为“世界羽毛球日”．在今年的世界羽毛球日，某主办方打算举办有关羽毛球的知识竞赛．比赛规则如下：比赛分为3轮，只有通过上一轮的比赛，才能进入下一轮比赛．甲、乙两人都计划参加这次有关羽毛球的知识竞赛，已知甲通过第一轮和第二轮比赛的概率均是

  3

  4

  ，通过第三轮比赛的概率是

  2

  3

  ，乙通过第一轮和第二轮比赛的概率均是

  2

  3

  ，通过第三轮比赛的概率是

  1

  2

  ，且甲、乙是否通过每轮比赛相互独立．
  （1）求甲三轮比赛全部通过的概率；
  （2）若通过第一轮和第二轮比赛，每轮可获得奖金100元，通过第三轮比赛，获得奖金200元，求甲、乙两人累计获得400元奖金的概率．
  组卷：35引用：1难度：0.7

  解析