2022-2023学年四川省泸州市高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知全集U={1，2，3，4，5，6，7，8}，集合A={2，3，5，6}，集合B={1，3，4，6，7}，则集合A∩∁_UB=（　　）

  A．{2，5}

  B．{3，6}

  C．{2，5，6}

  D．{2，3，5，6，8}
  组卷：2789引用：62难度：0.9

  解析

• 2．为了解某地区的中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男、女生视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是（　　）

  A．简单随机抽样	B．按性别分层随机抽样
  C．按学段分层随机抽样	D．其他抽样方法
  组卷：333引用：9难度：0.9

  解析

• 3．下列函数是幂函数，且在定义域内为增函数的是（　　）

  A．y=x2

  B．y=x3

  C． y = - x 1 2

  D．y=2x
  组卷：234引用：2难度：0.8

  解析

• 4．若复数z满足z（1+i）=1-i（i是虚数单位），则z的共轭复数

  z

  =（　　）

  A．-i

  B． - 2 i

  C．i

  D． 2 i
  组卷：249引用：18难度：0.9

  解析

• 5．设A=R，B={x|y=tanx}，则A是B的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分又不必要条件
  组卷：17引用：2难度：0.7

  解析

• 6．圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为（　　）

  A．7

  B．6

  C．5

  D．3
  组卷：497引用：14难度：0.7

  解析

• 7．已知

  α

  ∈

  （

  -

  π

  2

  ，

  0

  ）

  ，cosα=

  4

  5

  ，则tan

  α

  2

  =（　　）

  A．3

  B．-3

  C． 1 3

  D．- 1 3
  组卷：82引用：3难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．在平面四边形ABCD中（如图1），AB∥CD，CD⊥DE，BE=2CD，E是AB中点，现将△ADE沿DE翻折得到四棱锥A-BCDE（如图2），
  
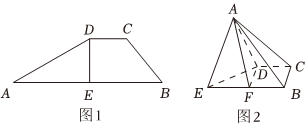
  （1）求证：平面AED⊥平面AEB；
  （2）图2中，若F是EB中点，试探究在平面AED内是否存在无数多个点P，都有直线CP∥平面ADF，若存在，请证明．
  组卷：51引用：1难度：0.5

  解析

• 22．已知函数f（x）=2^x+m•2^-x的图象关于原点对称．
  （1）判断函数f（x）在定义域上的单调性，并用单调性的定义证明；
  （2）设函数

  g

  （

  x

  ）

  =

  lo

  g

  a

  [

  4

  x

  +

  4

  -

  x

  +

  2

  -

  af

  （

  x

  ）

  ]

  （a＞0且a≠1）在[0，log₂3]上的最小值为1，求a的值．
  组卷：70引用：1难度：0.4

  解析