2023年河北省保定市部分高中高考数学三模试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知

  A

  =

  {

  x

  |

  lo

  g

  2

  1

  x

  ＜

  2

  ）

  ，B={x|x²-x-2≤0}，则（∁_RA）∩B=（　　）

  A． { x | - 1 ≤ x ≤ 1 4 }

  B． | x | - 2 ≤ x ≤ 1 4 }

  C．R

  D． { x | x ≥ 1 4 }
  组卷：56引用：1难度：0.7

  解析

• 2．设z=i²⁰²³-1（i 是虚数单位），则z²-2

  z

  =（　　）

  A．-2

  B．-2+4i

  C．2

  D．4-i
  组卷：29引用：1难度：0.8

  解析

• 3．已知直线l₁：ax-5y-1=0，l₂：3x-（a+2）y+4=0，“a=3”是“l₁∥l₂”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：79引用：5难度：0.8

  解析

• 4．已知随机变量ξ服从正态分布N（2，σ²），且P（ξ≤0）=0.2，则P（2＜ξ≤4）等于（　　）

  A．0.8

  B．0.6

  C．0.4

  D．0.3
  组卷：76引用：3难度：0.8

  解析

• 5．已知△ABC外接圆的半径为R，且

  a

  2

  -

  c

  2

  2

  R

  =

  （

  a

  -

  b

  ）

  sin

  B，sinB=2sinA，c=2，则△ABC的面积为（　　）

  A． 4 3

  B． 2 3 3

  C． 4 3 3

  D． 2 3
  组卷：146引用：3难度：0.6

  解析

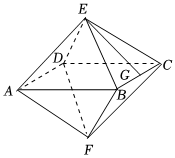• 6．正多面体被古希腊圣哲认为是构成宇宙的基本元素，加上它们的多种变体，一直是科学、艺术、哲学灵感的源泉之一．如图，该几何体是一个高为4的正八面体，G为BC的中点，则异面直线EG与BF所成角的正弦值为（　　）

  A． 3 6

  B． 3 2

  C． 6 3

  D． 33 6
  组卷：44引用：1难度：0.6

  解析

• 7．设O为坐标原点，点A（2，4），B在抛物线y²=2px（p＞0）上，F为焦点，M是线段BF上的点，且

  BM

  =

  2

  MF

  ，则当直线OM的斜率最大时，点F到OM的距离为（　　）

  A． 2 2

  B． 3 3

  C． 6 4

  D． 2 3 3
  组卷：125引用：1难度：0.4

  解析

四、解答题：本题共6小题，共70分.解答应写出必要的文字说明、证明过程及演算步骤.

• 21．设椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右顶点分别为A，B，离心率为e,且

  |

  AB

  |

  =

  8

  3

  3

  e

  =

  4

  ．
  （1）求椭圆C的标准方程；
  （2）设点P，Q为椭圆上异于A，B的两动点，记直线AP的斜率为k₁，直线QB的斜率为k₂，已知k₁=7k₂．直线PQ与x轴相交于点M，求△APM的面积的最大值．
  组卷：76引用：1难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  ax

  +

  1

  3

  x

  3

  ．
  （1）求函数f（x）的单调区间；
  （2）设g（x）=f（x）+2e^x+2cosx有两个极值点x₁，x₂，且x₁＜x₂．
  （i）求实数a的取值范围；
  （ii）求证：g（x₁）+g（x₂）＞8．
  组卷：94引用：3难度：0.6

  解析