当前位置：试卷中心 > 试卷详情

2018-2019学年湖南省株洲外国语学校九年级（上）月考数学试卷（12月份）

发布：2024/8/25 3:0:9

一、选择题（每小题有且只有一个正确答案，本题共10小题，每小题3分，共30分）

1．一种花粉颗粒直径约为0.0000065米，数字0.0000065用科学记数法表示为（　　）
A．0.65×10^-5 B．65×10^-7 C．6.5×10^-6 D．6.5×10^-5
组卷：1524引用：20难度：0.9
解析
2．下列运算一定正确的是（　　）
A．（m+n）²=m²+n² B．（mn）³=m³n³
C．（m³）²=m⁵ D．m•m²=m²
组卷：133引用：5难度：0.7
解析
3．已知两个有理数a,b,如果ab＜0且a+b＞0，那么（　　）
A．ab异号且正数的绝对值较大
B．a＜0，b＞0
C．ab同号
D．a＞0，b＞0
组卷：417引用：51难度：0.7
解析
4．已知反比例函数y=
2
k
-
3
x
的图象经过点（1，1），则k的值为（　　）
A．-1 B．0 C．1 D．2
组卷：779引用：5难度：0.7
解析
5．某商品打七折后价格为a元，则原价为（　　）
A．a元 B．
10
7
a元 C．30%a元 D．
7
10
a元
组卷：2680引用：22难度：0.9
解析
6．将抛物线y=-5x²+1向左平移1个单位长度，再向下平移2个单位长度，所得到的抛物线为（　　）
A．y=-5（x+1）²-1 B．y=-5（x-1）²-1
C．y=-5（x+1）²+3 D．y=-5（x-1）²+3
组卷：4933引用：73难度：0.9
解析
7．在同一平面直角坐标系中，函数y=
k
x
和y=kx-3的图象大致是（　　）
A． B． C． D．
组卷：2159引用：21难度：0.7
解析
8．已知关于x的分式方程
m
-
2
x
+
1
=1的解是负数，则m的取值范围是（　　）
A．m≤3 B．m≤3且m≠2 C．m＜3 D．m＜3且m≠2
组卷：4109引用：33难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共8小题，共66分，需要有必要的解答过程与步骤）

25．知识背景
当a＞0且x＞0时，因为（
x
-
a
x
）²≥0，所以x-2
a
+
a
x
≥0，从而x+
a
x
≥
2
a
（当x=
a
时取等号）．
设函数y=x+
a
x
（a＞0，x＞0），由上述结论可知：当x=
a
时，该函数有最小值为2
a
．
应用举例
已知函数为y₁=x（x＞0）与函数y₂=
4
x
（x＞0），则当x=
4
=2时，y₁+y₂=x+
4
x
有最小值为2
4
=4．
解决问题
（1）已知函数y₁=x+3（x＞-3）与函数y₂=（x+3）²+9（x＞-3），当x取何值时，
y
2
y
1
有最小值？最小值是多少？
（2）已知某设备租赁使用成本包含以下三部分：一是设备的安装调试费用，共490元；二是设备的租赁使用费用，每天200元；三是设备的折旧费用，它与使用天数的平方成正比，比例系数为0.001．若设该设备的租赁使用天数为x天，则当x取何值时，该设备平均每天的租赁使用成本最低？最低是多少元？
组卷：1067引用：3难度：0.3
解析
26．已知抛物线C₁：y=ax²过点（2，2）
（1）直接写出抛物线的解析式
；
（2）如图，△ABC的三个顶点都在抛物线C₁上，且边AC所在的直线解析式为y=x+b,若AC边上的中线BD平行于y轴，求
A
C
2
BD
的值；
（3）如图，点P的坐标为（0，2），点Q为抛物线上C₁上一动点，以PQ为直径作⊙M，直线y=t与⊙M相交于H、K两点是否存在实数t,使得HK的长度为定值？若存在，求出HK的长度；若不存在，请说明理由．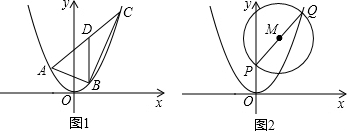
组卷：593引用：3难度：0.4
解析