2023-2024学年四川省成都市石室中学高三（上）开学数学试卷（理科）

一、选择题（本题共12道小题，每小题5分，共60分）

• 1．已知集合A={x∈N|-1≤x＜4}，B={x|x²-2x-3＜0}，则A∩B=（　　）

  A．{1，2}

  B．{0，1，2}

  C．{1，2，3}

  D．{0，1，2，3}
  组卷：87引用：7难度：0.7

  解析

• 2．若复数z满足z•（1+3i）=2-4i,则|z|=（　　）

  A． 2 2

  B．1

  C． 2

  D．2
  组卷：28引用：3难度：0.8

  解析

• 3．函数

  f

  （

  x

  ）

  =

  x

  2

  -

  3

  x

  e

  x

  的图象大致是（　　）

  A．	B．
  C．	D．
  组卷：39引用：4难度：0.8

  解析

• 4．已知实数x,y满足a^x＜a^y（0＜a＜1），则下列关系式恒成立的是（　　）

  A． 1 x 2 + 1 ＞ 1 y 2 + 1	B．ln（x2+1）＞ln（y2+1）
  C．sinx＞siny	D．x3＞y3
  组卷：2036引用：51难度：0.9

  解析

• 5．若a＞0，b＞0，lga+lgb=lg（a+b），则a+b的最小值为（　　）

  A．8

  B．6

  C．4

  D．2
  组卷：1197引用：11难度：0.9

  解析

• 6．已知命题p：若ac²＞bc²，则a＞b；命题q：在△ABC中，sinA=sinB是A=B的必要不充分条件，则下列命题为真命题的是（　　）

  A．￢p∨q

  B．￢（p∨q）

  C．p∧q

  D．p∧￢q
  组卷：8引用：3难度：0.8

  解析

• 7．某四棱锥的三视图如图所示，则该四棱锥的体积是（　　）
  

  A． 1 4

  B． 1 2

  C．1

  D．2
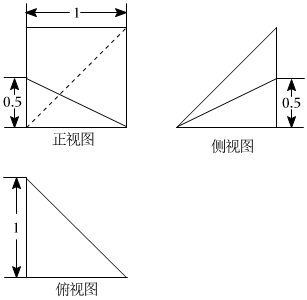  组卷：33引用：3难度：0.5

  解析

三、解答题（本题共6道小题，17题10分，其余各题12分，共70分）

• 21．设f（x）=lnx.
  （1）证明：y=f（x）的图象与直线

  y

  =

  -

  x

  e

  有且只有一个横坐标为α的公共点，且

  α

  ∈

  （

  1

  e

  ，

  1

  ）

  ；
  （2）求所有的实数k,使得直线y=kx与函数y=f²（x）的图象相切；
  （3）设

  a

  ,

  b

  ,

  c

  ∈

  （

  （

  α

  e

  ）

  2

  ，

  +

  ∞

  ）

  （其中α由（1）给出），且a+b+c=3，g（x）=lnx+2，求g²（a）+g²（b）+g²（c）的最大值．
  组卷：72引用：5难度：0.2

  解析

• 22．在直角坐标系xOy中，直线的方程为x+y=a（a＞0），曲线C的参数方程为

  x = 1 + cosθ

  y = sinθ

  （θ为参数），点P，Q分别在直线和曲线C上运动，|PQ|的最小值为

  3

  2

  2

  -

  1

  ．
  （I）求a的值；
  （II）以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，射线

  l

  1

  ：

  θ

  =

  α

  （

  p

  ≥

  0

  ，

  0

  ＜

  α

  ＜

  π

  2

  ）

  与曲线C交于不同的两点O，A，与直线交于点B，若|OA|=|AB|，求α的值．
  组卷：156引用：6难度：0.3

  解析