2022-2023学年安徽省安庆市宿松中学高二（上）开学数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合M={-1，0，1，2}，集合N={x∈R|x²=x}，则M∩N=（　　）

  A．{1}

  B．{0}

  C．{0，1}

  D．{-1，0}
  组卷：57引用：3难度：0.9

  解析

• 2．若复数z=

  i

  2

  -

  i

  （i是虚数单位）的共轭复数是

  z

  ，则z-

  z

  =（　　）

  A．- 2 5

  B．- 4 5 i

  C．- 1 5 - 2 5 i

  D． 4 5 i
  组卷：61引用：4难度：0.8

  解析

• 3．已知m,n是平面α内的两条不同的直线，则“直线l⊥m且l⊥n”是“l⊥α”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：159引用：2难度：0.7

  解析

• 4．若

  cos

  2

  α

  sin

  （

  α

  -

  π

  4

  ）

  =-

  2

  2

  ，则sinα•cosα=（　　）

  A． 3 8

  B．- 3 8

  C． 3 4

  D．- 3 4
  组卷：168引用：2难度：0.7

  解析

• 5．某快递公司为降低新冠肺炎疫情带来的经济影响，引进智能机器人分拣系统，以提高分拣效率和降低物流成本．已知购买x台机器人的总成本为P（x）=

  1

  600

  x

  2

  +x+150（单位：万元）．若要使每台机器人的平均成本最低，则应买机器人（　　）

  A．100台

  B．200台

  C．300台

  D．400台
  组卷：303引用：4难度：0.8

  解析

• 6．已知向量

  a

  是非零向量，

  b

  是单位向量，

  a

  ，

  b

  的夹角为120°，且

  a

  ⊥（

  a

  +

  b

  ），则|

  a

  |=（　　）

  A． 1 2

  B． 2 2

  C．1

  D．2
  组卷：244引用：5难度：0.8

  解析

• 7．已知实数a,b,c满足3×2^a-2^b+1=0，且a=c+log₂（x²-x+2）（x∈R），则a,b,c的大小关系是（　　）

  A．a＞b＞c

  B．b＞a＞c

  C．a＞c＞b

  D．c＞b＞a
  组卷：38引用：3难度：0.6

  解析

四、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.

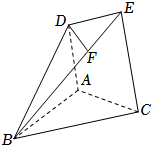• 21．如图，在四棱锥B-ACED中，AD∥CE，且AD=

  2

  3

  CE，F是棱BE上一点，且满足BF=2FE．
  （1）证明：DF∥平面ABC；
  （2）若三棱锥B-ADF的体积是4，△ABC的面积是2

  2

  ，求点F到平面ABC的距离．
  组卷：53引用：3难度：0.6

  解析

• 22．已知函数f（x）=

  lo g 2 （ x + 1 ） （ x ≤ m ）

  2 x - 3 （ x ＞ m ）

  ，其中m＞0．若存在实数b,使得关于x的方程f（x）=b有两个不同的实数根．
  （1）求m的整数值；
  （2）设函数g（x）=x²+a|x-t|，t取m的最大整数值．若g（x）在[0，+∞）上单调递增，求实数a的取值范围．
  组卷：75引用：3难度：0.5

  解析