2023-2024学年山东省日照市校际联考高二（上）月考数学试卷（8月份）

一、单项选择题：本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．设集合M={1，3，5，7，9}，N={x|2x＜9}，则M∩N=（　　）

  A．{1，3}

  B．{1，3，5}

  C．{1，3，5，7}

  D．{1，3，5，7，9}
  组卷：43引用：3难度：0.7

  解析

• 2．若命题“∃x∈R，使得x²+2ax+1＜0”是假命题，则实数a的取值范围是（　　）

  A．-1＜a＜1

  B．a≤-1或a≥1

  C．-1≤a≤1

  D．a＜-1或a＞1
  组卷：265引用：9难度：0.7

  解析

• 3．用二分法求方程

  lo

  g

  4

  x

  -

  1

  2

  x

  =

  0

  近似解时，所取的第一个区间可以是（　　）

  A．（0，1）

  B．（1，2）

  C．（2，3）

  D．（3，4）
  组卷：268引用：7难度：0.8

  解析

• 4．函数f（x）=

  （

  1

  -

  e

  2

  x

  ）

  cosx

  e

  x

  的部分图象大致为（　　）

  A．

  B．

  C．

  D．​
  组卷：159引用：6难度：0.7

  解析

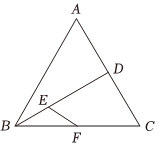• 5．如图，在边长为2的等边△ABC中，点E为中线BD的三等分点（靠近点B），点F为BC的中点，则

  FE

  •

  FC

  =（　　）

  A． - 3 4

  B． - 1 2

  C． 3 4

  D． 1 2
  组卷：275引用：5难度：0.6

  解析

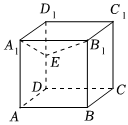• 6．如图，在棱长为a的正方体ABCD-A₁B₁C₁D₁中，点E为棱DD₁的中点，则点A到平面A₁B₁E的距离为（　　）

  A． 5 a

  B． 5 5 a

  C． 2 5 5 a

  D． 3 5 5 a
  组卷：97引用：4难度：0.6

  解析

• 7．已知定义在R上的函数f（x）满足f（x+3）=f（x-3），且y=f（x+3）为偶函数，若f（x）在（0，3）上单调递减，则下面结论正确的是（　　）

  A．f（-4.5）＜f（3.5）＜f（12.5）

  B．f（3.5）＜f（12.5）＜f（-4.5）

  C．f（12.5）＜f（3.5）＜f（-4.5）

  D．f（3.5）＜f（-4.5）＜f（12.5）
  组卷：146引用：7难度：0.6

  解析

四、解答题：共70分。解答应写出文字说明，证明过程或演算步骤。

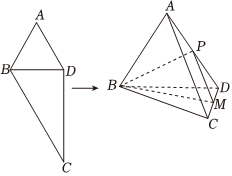• 21．已知平面四边形ABCD，AB=AD=2，∠BAD=60°，∠BCD=30°，现将△ABD沿BD边折起，使得平面ABD⊥平面BCD，此时AD⊥CD，点P为线段AD的中点，点M在线段CD上．
  （1）求证：BP⊥平面ACD；
  （2）若直线BM与平面ACD所成角的正弦值为

  21

  7

  ，求二面角P-BM-D的平面角的余弦值．
  组卷：58引用：3难度：0.4

  解析

• 22．已知f₁（x）=|x-2a+1|，f₂（x）=|x-a|+1，x∈R．
  （1）若a=3，求函数

  y

  =

  e

  f

  1

  （

  x

  ）

  +

  e

  f

  2

  （

  x

  ）

  在x∈[3，5]上的最小值；
  （2）若|f₁（x）-f₂（x）|=f₂（x）-f₁（x）对于任意的实数x∈R恒成立，求a的取值范围；
  （3）当0≤a≤6时，求函数

  g

  （

  x

  ）

  =

  f

  1

  （

  x

  ）

  +

  f

  2

  （

  x

  ）

  2

  -

  |

  f

  1

  （

  x

  ）

  -

  f

  2

  （

  x

  ）

  |

  2

  在x∈[2，8]上的最小值．
  组卷：31引用：3难度：0.3

  解析