2023-2024学年广东省阳江市江城区八年级（上）期中数学试卷
发布：2024/10/3 18:0:2
一、选择题：本大题共10小题，每小题3分，共30分.在每小题列出的四个选项中，只有一项是符合题目要求的.
-
1．在以下绿色食品、节能、节水、回收四个标志中，是轴对称图形的是（ ）
组卷：172引用：9难度：0.7 -
2．现有两根木棒，它们的长分别为40cm和60cm,若要钉成一个三角形木架，则第三根木棒的长可以选取（ ）
组卷：16引用：1难度：0.8 -
3．图中能表示△ABC的BC边上的高的是（ ）
组卷：3385引用：55难度：0.9 -
4．一个多边形的内角和等于900°，则这个多边形的边数是（ ）
组卷：34引用：1难度：0.8 -
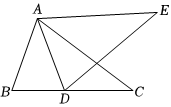5．如图，若△ABC≌△ADE，则下列结论一定成立的是（ ）组卷：85引用：2难度：0.5 -
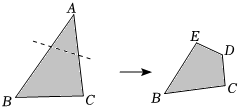6．如图，将三角形纸片剪掉一角得四边形，设△ABC与四边形BCDE的外角和的度数分别为α，β，则正确的是（ ）组卷：2519引用：29难度：0.6 -
7．如图，在△ABC中，∠A=78°，∠ACD是△ABC的一个外角，∠EBC=∠ABC，∠ECD=13∠ACD，则∠E为（ ）13组卷：1978引用：8难度：0.7 -
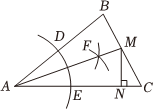8．如图，在△ABC中，AB=4，AC=5，以点A为圆心，任意长为半径画弧，分别交AB，AC于点D和E，再分别以点D，E为圆心，大于长为半径画弧，两弧交于点F，连接AF并延长交BC于点M，作MN⊥AC于点N．若MN=2，则△ABM的面积为（ ）12DE组卷：86引用：1难度：0.5
三、解答题：本大题共9小题，共72分.解答应写出文字说明、证明过程或演算步骤.
-
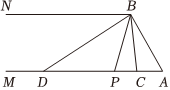24．【问题情境】：在综合实践课上，老师组织班上的同学开展了探究两角之间数量关系的数学活动，如图，已知射线AM∥BN，连接AB，点P是射线AM上的一个动点（与点A不重合），BC，BD分别平分∠ABP和∠PBN，且分别交射线AM于点C，D．
【探索发现】：
（1）当∠A=60°时，求证：∠CBD=∠A；
（2）“快乐小组”经过探索后发现：不断改变∠A的度数，∠CBD与∠A始终存在某种数量关系．
①当∠A=40°时，∠CBD=度；
②当∠A=x°时，∠CBD=度（用含x的代数式表示）；
【操作探究】：
（3）“智慧小组”利用量角器量出∠APB和∠ADB的度数后，探究二者之间的数量关系．他们惊奇地发现，当点P在射线AM上运动时，无论点P在AM上的什么位置，∠APB与∠ADB之间的数量关系都保持不变．请写出它们的关系，并说明理由．组卷：939引用：7难度：0.8 -
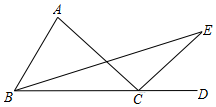
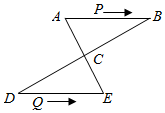25．如图，AE与BD相交于点C，AC=EC，BC=DC，AB=4cm,点P从点A出发，沿A→B→A方向以3cm/s的速度运动，点Q从点D出发，沿D→E方向以1cm/s的速度运动，P、Q两点同时出发．当点P到达点A时，P、Q两点同时停止运动．设点P的运动时间为t（s）．
（1）求证：AB∥DE．
（2）写出线段AP的长（用含t的式子表示）．
（3）连接PQ，当线段PQ经过点C时，求t的值．组卷：3261引用：11难度：0.5
