2023年湖南省益阳市安化县中考数学二模试卷

一、选择题（本题共10个小题，每小题4分，共40分.每小题都给出A、B、C、D四个选项，其中只有一项是符合题目要求的）

• 1．-

  1

  2

  的相反数是（　　）

  A． 1 2

  B．2

  C．-2

  D．- 1 2
  组卷：3015引用：744难度：0.9

  解析

• 2．计算（-2m²）³的结果为（　　）

  A．-6m⁵

  B．8m⁶

  C．-8m⁶

  D．6m⁵
  组卷：175引用：1难度：0.5

  解析

• 3．不等式组

  9 - 3 x ＞ 0

  7 - 2 x ≤ 5

  的解集在以下数轴表示中正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：860引用：17难度：0.8

  解析

• 4．要使

  x

  -

  2022

  x

  -

  2022

  在实数范围内有意义，则x的值可能为（　　）

  A．2023

  B．2021

  C．-2022

  D．2022
  组卷：201引用：3难度：0.7

  解析

• 5．已知一元二次方程x²-4x-3=0的两根分别为m,n,则3m+3n-mn的值是（　　）

  A．15

  B．13

  C．-9

  D．9
  组卷：769引用：6难度：0.6

  解析

• 6．某校举办才艺表演活动，需要从学生中挑选表演活动的主持人．若有2名男生和2名女生作为学生候选人，从这4名学生中随机抽取2名作为主持人，则恰好抽到1名男生和1名女生的概率是（　　）

  A．. 1 3

  B．. 1 2

  C． 2 3

  D．. 3 4
  组卷：39引用：2难度：0.7

  解析

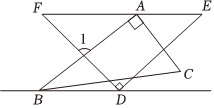• 7．已知直线BD∥EF，将两个直角三角板按如图所示的位置摆放，若∠CBD=10°，则∠1=​（　　）

  A．75°

  B．80°

  C．85°

  D．95°
  组卷：31引用：2难度：0.6

  解析

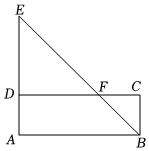• 8．如图，F是矩形ABCD的边CD上一点，射线BF交AD的延长线于点E，已知DE=2BC=4，CD=6，求BF的长（　　）

  A． 2 2

  B．3

  C． 13

  D． 5
  组卷：241引用：2难度：0.7

  解析

三、解答题（本题共8个小题，共78分）

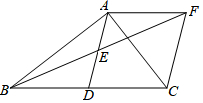• 25．如图，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．
  （1）求证：△AEF≌△DEB；
  （2）若∠BAC=90°，试判断四边形ADCF的形状，并证明你的结论；
  （3）在（2）情况下，如果AD=2，∠ADC=90°，点M在AC线段上移动，当MB+MD有最小值时，求AM的长度．
  组卷：723引用：6难度：0.3

  解析

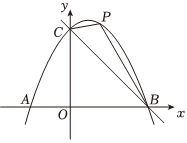• 26．如图，抛物线y=ax²+bx+6与x轴交于A（-2，0），B（6，0）两点，与y轴交于点C，对称轴l与x轴交于点F，P是直线BC上方抛物线上一动点，连接PB，PC．
  （1）求抛物线的表达式．
  （2）当四边形ACPB面积最大时，求点P的坐标；
  （3）在（2）的条件下，连接PF，E是x轴上一动点，在抛物线上是否存在点Q，使得以F，P，E，Q为顶点的四边形是平行四边形．若存在，请求出点Q的坐标；若不存在，说明理由．
  组卷：125引用：1难度：0.5

  解析