2022-2023学年江西省上饶四中八年级（下）期中数学试卷
发布：2024/7/26 8:0:9
一．选择题（本大题共6小题，每小题3分，共18分）
-
1．下列二次根式中是最简二次根式的是（ ）
组卷：443引用：7难度：0.7 -
2．下列运算正确的是（ ）
组卷：384引用：6难度：0.8 -
3．△ABC中，∠A，∠B，∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是（ ）
组卷：971引用：13难度：0.9 -
4．若
是整数，则正整数a的最小值是（ ）54a组卷：983引用：8难度：0.8 -
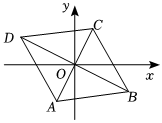5．如图，菱形ABCD的对角线交于原点O，若点B的坐标为（4，m），点D的坐标为（n,2），则m+n的值为（ ）组卷：1786引用：15难度：0.8 -
6．已知下列命题
①一组对边平行且相等的四边形是平行四边形；
②两条对角线互相垂直且相等的四边形是正方形；
③一组对边平行且两条对角线相等的四边形是矩形；
④两条对角线互相垂直的平行四边形是菱形．
其中正确的命题的个数是（ ）组卷：1344引用：9难度：0.9
二．填空题（本大题共6小题，每小题3分，共18分）
-
7．若二次根式
在实数范围内有意义，则x的取值范围是 ．x+4组卷：169引用：7难度：0.9
五、解答题（本大题共2小题，每小题9分，共18分）
-
22．我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”．数学中，数和形是两个最主要的研究对象，它们之间有着十分密切的联系，在一定条件下，数和形之间可以相互转化，相互渗透．
某校数学兴趣小组，在学习完勾股定理和实数后，进行了如下的问题探索与分析：
【提出问题】已知0＜x＜1，求的最小值1+x2+1+（1-x）2
【分析问题】由勾股定理，可以通过构造直角三角形的方法，来分别表示长度为和1+x2的线段，将代数求和转化为线段求和问题．1+（1-x）2
【解决问题】
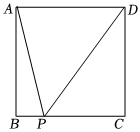
（1）如图，我们可以构造边长为1的正方形ABCD，P为BC边上的动点．设BP=x,则PC=1-x.
则=线段 +线段 ；1+x2+1+（1-x）2
（2）在（1）的条件下，已知0＜x＜1，求的最小值；1+x2+1+（1-x）2
（3）【应用拓展】应用数形结合思想，求的最大值．x2+9-（x-6）2+1组卷：162引用：3难度：0.2
六、解答题（本大题共1小题，共12分）
-
23．（1）【母题呈现】如图1，DE是△ABC的中位线，以AB为斜边作Rt△ABF，∠AFB=90°，∠ABF=30°，求证：DE=AF．
（2）【母题变式】如图2，DE是△ABC的中位线，分别以AB、AC为斜边作Rt△ABF和Rt△ACG，∠ABF=∠CAG=30°，∠AFB=∠AGC=90°，作EH⊥AC交CG的延长线于点H，FG与DH交于点O．
①求证：FG=DH；
②求∠FOD的度数．
（3）【拓展应用】如图3，在△ABC中，分别以AB、AC为斜边作Rt△ABF和Rt△ACG，∠ABF=∠CAG=30°，∠AFB=∠AGC=90°，点P是线段BC上一点，且CP=BC，连接PF、PG，请写出PF与PG之间的一个等量关系，并证明．14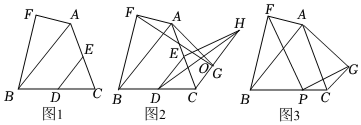
组卷：341引用：2难度：0.4
