2022-2023学年四川省内江市资中二中高二（下）入学数学试卷（理科）

一、选择题

• 1．已知三维数组

  a

  =

  （

  2

  ，-

  1

  ，

  0

  ）

  ，

  b

  =

  （

  1

  ，

  k

  ,

  7

  ）

  ，且

  a

  ⊥

  b

  ，则实数k的值为（　　）

  A．-2

  B．2

  C． 2 7

  D．-9
  组卷：43引用：2难度：0.8

  解析

• 2．从装有2个红球和2个黑球的口袋内任取2个球，那么互斥而不对立的两个事件是（　　）

  A．至少有一个黑球与都是红球

  B．至少有一个红球与都是红球

  C．至少有一个红球与至少有1个黑球

  D．恰有1个红球与恰有2个红球
  组卷：175引用：4难度：0.8

  解析

• 3．设α、β是两个不同的平面，m、n是两条不同的直线，且m⊂α，n⊂β，下列命题正确的是（　　）

  A．如果m∥β，那么α∥β	B．如果α∥β，那么m∥n
  C．如果m⊥β，那么α⊥β	D．如果α⊥β，那么m⊥β
  组卷：32引用：4难度：0.7

  解析

• 4．设a∈R，若直线l₁：ax+2y-8=0与直线l₂：x+（a+1）y+5=0平行，则a的值为（　　）

  A．1

  B．-2

  C．1或-2

  D．- 2 3
  组卷：180引用：5难度：0.8

  解析

• 5．过点P（1，1）可以向圆x²+y²+2x-4y+k-2=0引两条切线，则k的范围是（　　）

  A．k＞2

  B．0＜k＜7

  C．k＜7

  D．2＜k＜7
  组卷：205引用：3难度：0.7

  解析

• 6．在三棱柱ABC-A₁B₁C₁中，△ABC是等边三角形，AA₁⊥平面ABC，AA₁=AB=2，D，E，F分别是BB₁，AA₁，A₁C₁的中点，则直线EF与CD所成角的余弦值为（　　）

  A． 2 2

  B． 1 2

  C．0

  D． - 1 2
  组卷：367引用：5难度：0.8

  解析

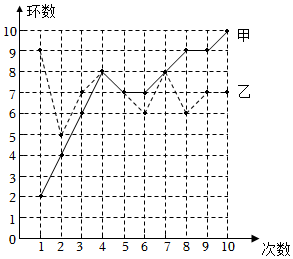• 7．甲、乙两人在相同条件下各打靶10次，每次打靶的成绩情况如图所示：下列说法错误的是（　　）

  A．从平均数和方差相结合看，甲波动比较大，乙相对比较稳定

  B．从折线统计图上两人射击命中环数走势看，甲更有潜力

  C．从平均数和命中9环及9环以上的次数相结合看，甲成绩较好

  D．从平均数和中位数相结合看，乙成绩较好
  组卷：145引用：7难度：0.7

  解析

三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．如图，直三棱柱ABC-A₁B₁C₁的体积为4，△A₁BC的面积为

  2

  2

  ．
  （1）求A到平面A₁BC的距离；
  （2）设D为A₁C的中点，AA₁=AB，平面A₁BC⊥平面ABB₁A₁，求二面角A-A₁C-B的大小．
  组卷：52引用：2难度：0.5

  解析

• 22．已知点P（0，2），设直线l：y=kx+b（k,b∈R）与圆C：x²+y²=4相交于异于点P的A，B两点．
  （Ⅰ）若

  PA

  •

  PB

  =0，求b的值；
  （Ⅱ）若|AB|=2

  3

  ，且直线l与两坐标轴围成的三角形的面积为

  2

  3

  3

  ，求直线l的斜率k的值；
  （Ⅲ）当|PA|•|PB|=4时，是否存在一定圆M，使得直线l与圆M相切？若存在，求出该圆的标准方程；若不存在，请说明理由．
  组卷：108引用：2难度：0.1

  解析