2023-2024学年上海市浦东新区洋泾中学高三（上）开学数学试卷（9月份）

一、填空题（本大题共12题，满分54分，第1～6题每题4分，第7～12题每题5分）

• 1．设集合M={x|0＜x＜4}，

  N

  =

  {

  x

  |

  1

  3

  ≤

  x

  ≤

  5

  }

  ，则M∩N=

  ．
  组卷：73引用：3难度：0.9

  解析

• 2．抛物线y²=8x的焦点到准线的距离是

  ．
  组卷：223引用：18难度：0.9

  解析

• 3．电视台连续播放6个广告，其中含4个不同的商业广告和2个不同的公益广告，要求首尾必须播放公益广告，则共有

  种不同的播放方式（结果用数值表示）．
  组卷：344引用：6难度：0.7

  解析

• 4．已知角α的顶点是坐标原点，始边与x轴的正半轴重合，它的终边过点

  P

  （

  -

  3

  5

  ，

  4

  5

  ）

  ．则cos2α=

  ．
  组卷：198引用：9难度：0.7

  解析

• 5．若正方形ABCD的边长为1，记

  AB

  =

  a

  ，

  BC

  =

  b

  ，

  AC

  =

  c

  ，则|

  a

  +2

  b

  -3

  c

  |=

  ．
  组卷：352引用：2难度：0.7

  解析

• 6．已知函数f（x）是定义在R上的周期为2的奇函数．当0＜x≤1时，f（x）=x³-ax+1，则实数a的值等于

  ．
  组卷：792引用：2难度：0.5

  解析

• 7．关于x的不等式x²-（a+1）x+a＜0的解集中恰有两个整数，则实数a的取值范围是

  ．
  组卷：133引用：5难度：0.6

  解析

三、解答题（本大题共5题，满分76分）

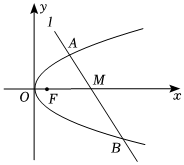• 20．设抛物线Γ：y²=4x的焦点为F，经过x轴正半轴上点M（m,0）的直线l交Γ于不同的两点A和B．
  （1）若|FA|=3，求A点的坐标；
  （2）若m=2，求证：原点O总在以线段AB为直径的圆的内部；
  （3）若|FA|=|FM|，且直线l₁∥l,l₁与Γ有且只有一个公共点E，问：△OAE的面积是否存在最小值？若存在，求出最小值，并求出M点的坐标；若不存在，请说明理由．
  （三角形面积公式：在△ABC中，设

  CA

  =

  a

  =

  （

  x

  1

  ，

  y

  1

  ）

  ，

  CB

  =

  b

  =

  （

  x

  2

  ，

  y

  2

  ）

  ，则△ABC的面积为

  S

  =

  1

  2

  |

  a

  |

  2

  |

  b

  |

  2

  -

  （

  a

  •

  b

  ）

  2

  =

  1

  2

  |

  x

  1

  y

  2

  -

  x

  2

  y

  1

  |

  ）．
  组卷：45引用：1难度：0.5

  解析

• 21．已知函数f（x）=（ax²+x+2）e^x（a≥0），其中e是自然对数的底数．
  （1）当a=0时，求曲线f（x）在点（0，f（0））处的切线方程；
  （2）若函数f（x）在[-2，2]上是严格递增函数，求a的取值范围；
  （3）当a=1时，求整数t的所有值，使方程f（x）=x+4在[t,t+1]上有解．
  组卷：49引用：2难度：0.3

  解析