2022-2023学年黑龙江省牡丹江第一高级中学高一(下)月考数学试卷(4月份)
发布:2024/6/29 8:0:10
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。)
-
1.设(1+i)z=3+i,则|z|=( )
组卷:232引用:7难度:0.8 -
2.已知向量
,a满足|b|=2|b|=2,a=1,则向量a•b的夹角为( )a,b组卷:45引用:1难度:0.8 -
3.已知平行四边形ABCD的顶点A(-1,-2),B(3,-1),C(5,6),则顶点D的坐标为( )
组卷:74引用:1难度:0.8 -
4.如图,在平行四边形ABCD中,E是BC的中点,
,则AE=3AF=( )DF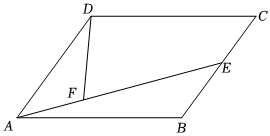 组卷:281引用:4难度:0.8
组卷:281引用:4难度:0.8 -
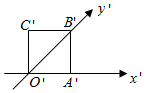 5.如图所示,正方形O′A′B′C′的边长为1,它是水平放置的一个平面图形的直观图,则原图形的周长是( )组卷:2754引用:47难度:0.9
5.如图所示,正方形O′A′B′C′的边长为1,它是水平放置的一个平面图形的直观图,则原图形的周长是( )组卷:2754引用:47难度:0.9 -
6.若O是△ABC所在平面上一定点,H,N,Q在△ABC所在平面内,动点P满足
=OP,λ∈(0,+∞)则直线AP一定经过△ABC的____心,点H满足OA+λ(AB|AB|+AC|AC|),则H是△ABC的____心,点N满足|HA|=|HB|=|HC|+NA+NB=0,则N是△ABC的____心,点Q满足NC,则Q是△ABC的____心,下列选项正确的是( )QA•QB=QB•QC=QC•QA组卷:164引用:1难度:0.5 -
7.已知对任意平面向量
=(x,y),把AB绕其起点沿逆时针方向旋转θ角得到向量AB=(xcosθ-ysinθ,xsinθ+ycosθ),叫做把点B绕点A沿逆时针方向旋转θ角得到点P.已知平面内点A(2,1),点B(2+t,1-t),AP,|AB|=22•AB>0,点B绕点A沿逆时针方向旋转OA得到点P,则下列结论错误的是( )π3组卷:45引用:1难度:0.5
四、解答题(本题共6小题,共70分,其中第17题10分,其它每题12分,解答应写出文字说明、证明过程或演算步骤。)
-
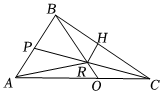 21.在△ABC中,P为AB的中点,O在边AC上,BO交CP于R,且,设AB=|AO|=2|OC|,AC=a.b
21.在△ABC中,P为AB的中点,O在边AC上,BO交CP于R,且,设AB=|AO|=2|OC|,AC=a.b
(1)试用,a表示b;AR
(2)若,求∠ARB的余弦值;|a|=2,|b|=1,<a,b>=60°
(3)若H在BC上,且RH⊥BC,设,若|a|=2,|b|=1,θ=<a,b>,求θ∈[π3,2π3]的取值范围.|CH||CB|组卷:377引用:21难度:0.5 -
22.在锐角△ABC中,设角A,B,C的对边分别为a,b,c,且a=4,
.cosA=35
(1)求的值;5b-3ccosC
(2)求的取值范围.|AB+AC|-AB•AC组卷:59引用:4难度:0.5


