2023-2024学年湖北省武汉市第三寄宿中学九年级（上）月考数学试卷（10月份）

一、选择题（每小题3分，共30分.）

• 1．下列方程中，关于x的一元二次方程的是（　　）

  A．ax2+bx+c=0	B．（x-1）2=x2+3x+2
  C．x2=x+1	D．2x2- 1 x +1=0
  组卷：110引用：8难度：0.9

  解析

• 2．一元二次方程3x²+1=6x的一次项系数为6，二次项系数和常数项分别为（　　）

  A．3，1

  B．-3，-1

  C．3，-1

  D．-3x2，-1
  组卷：838引用：8难度：0.8

  解析

• 3．用配方法解方程x²-6x+8=0时，方程可变形为（　　）

  A．（x-3）2=1

  B．（x-3）2=-1

  C．（x+3）2=1

  D．（x+3）2=-1
  组卷：302引用：16难度：0.7

  解析

• 4．某超市一月份的营业额为100万元，第一季度的营业额共800万元．如果平均每月增长率为x,则所列方程应为（　　）

  A．100（1+x）2=800

  B．100+100×2x=800

  C．100+100×3x=800

  D．100[1+（1+x）+（1+x）2]=800
  组卷：1520引用：30难度：0.9

  解析

• 5．设a、b为x²+x-2011=0的两个实根，则a³+a²+3a+2014b=（　　）

  A．2014

  B．-2014

  C．2011

  D．-2011
  组卷：920引用：5难度：0.8

  解析

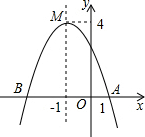• 6．如图，函数y=ax²+bx+c（a≠0）的图象与x轴相交于A、B两点，顶点为点M．则下列说法不正确的是（　　）

  A．a＜0

  B．当x=-1时，函数y有最小值4

  C．对称轴是直线=-1

  D．点B的坐标为（-3，0）
  组卷：225引用：5难度：0.9

  解析

• 7．在同一坐标系中，一次函数y=ax+1与二次函数y=x²+a的图象可能是（　　）

  A．

  B．

  C．

  D．
  组卷：4417引用：53难度：0.7

  解析

• 8．在平面直角坐标系中，如果抛物线y=2x²不动，而把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是（　　）

  A．y=2（x-2）2+2	B．y=2（x-2）2-2
  C．y=2（x+2）2-2	D．y=2（x+2）2+2
  组卷：143引用：1难度：0.9

  解析

三、解答题：（共8题，共72分）

• 23．综合与实践
  问题情境
  数学活动课上，老师发给每名同学一个等腰三角形纸片ABC，AB=AC，∠BAC＞90°，要求同学们将纸片沿一条直线折叠，探究图形中的结论．
  问题发现
  奋进小组在边AC上取一点D，连接BD，将这个纸片沿BD翻折，点A的对应点为E，如图1所示．
  如图2，小明发现，当点E落在边BC上时，∠DEC=2∠ACB．
  如图3，小红发现，当点D是AC的中点时，连接CE，若已知AB和CE的长，则可求BD的长．
  ……
  问题提出与解决
  奋进小组根据小明和小红的发现，讨论后提出问题1，请你解答．
  问题1：在△ABC中，AB=AC，∠BAC＞90°，点D是边AC上一点，将△ABD沿BD翻折得到△EBD．
  （1）如图2，当点E在边BC上时，求证：∠DEC=2∠ACB．
  （2）如图3，当点D是AC的中点时，连接CE，若AB=4，CE=3，求BD的长．
  拓展延伸
  小刚受到探究过程的启发，将等腰三角形的顶角改为锐角，尝试画图，并提出问题2，请你解答．
  问题2：如图4，点D是△ABC外一点，AB=AC=BD=4，CD=1，∠ABD=2∠BDC，求BC的长．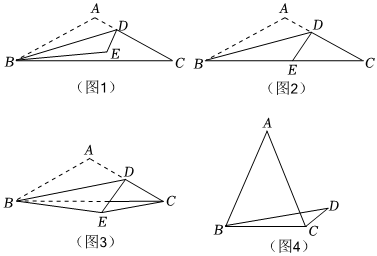
  
  组卷：248引用：5难度：0.1

  解析

• 24．如图1，在平面直角坐标系xOy中，已知抛物线y=ax²+bx-3（a≠0）与x轴交于点A（-1，0），B（3，0），与y轴交于点C，连接BC．
  （1）求抛物线的解析式．
  （2）P是直线BC下方抛物线上的一点，连接PB、PC、PO，PO交BC于D，S_△CPD：S_△BPD=1：2，求点D的坐标．
  （3）如图2，若动直线l与抛物线交于M，N两点（直线l与BC不重合），连接CN，BM，直线CN与BM交于点Q．当MN∥BC时，点Q的横坐标是否为定值，请说明理由．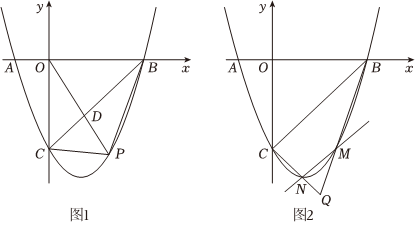
  组卷：390引用：1难度：0.2

  解析