当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省盐城初级中学康居路校区七年级（上）月考数学试卷（12月份）

发布：2024/8/19 0:0:1

一、选择题（本大题共有8小题，每小题2分，共16分）

1．下列各式中，最符合代数式书写要求的是（　　）
A．3m B．1
2
3
mn C．-1mn D．2÷3n
组卷：206引用：3难度：0.8
解析
2．下列运算正确的是（　　）
A．2x+y=2xy B．3x-x=3
C．3x³+2x²=5x⁵ D．-xy²+2xy²=xy²
组卷：79引用：3难度：0.8
解析
3．下列方程中是一元二次方程的是（　　）
A．ax²+bx+c=0 B．x-1=7 C．7x²+6=0 D．2x²-5y=0
组卷：526引用：13难度：0.9
解析
4．下列方程变形正确的是（　　）
A．由3+x=7，得x=7+3 B．由3（x-1）=8，得3x-1=8
C．由3-x=7，得x=7-3 D．由
x
3
=
7
，得x=21
组卷：379引用：4难度：0.9
解析
5．已知x=2是关于x的一元一次方程mx+2=0的解，则m的值为（　　）
A．-1 B．0 C．1 D．2
组卷：1241引用：33难度：0.9
解析
6．小敏把一商品按标价的九折出售（即优惠10%），仍可获利30元，若这种商品的进价为60元，则该商品的标价为（　　）
A．100元 B．90元 C．110元 D．120元
组卷：339引用：4难度：0.8
解析
7．一个两位数，个位数字与十位数字的和为9，如果将个位数字与十位数字对调后所得新数比原数小9，则原两位数是（　　）
A．45 B．27 C．72 D．54
组卷：2916引用：7难度：0.5
解析
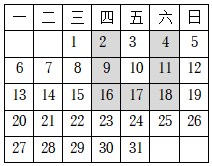8．如图，表中给出的是某月的月历，任意选取“U”型框中的7个数（如阴影部分所示），请你运用所学的数学知识来研究，发现这7个数的和不可能的是（　　）
A．78 B．70 C．84 D．105
组卷：398引用：9难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共有7小题，共64分）

25．【阅读理解】
在学习第3章《代数式》过程中，我们曾把5（x-2y）-3（2y-x）+8（2m+3n+1）-4（2m+4n）中的“x-2y”看成一个字母a,把“2m+3n”看成另一个字母b,将这个代数式简化为5a-3（-a）+8（b+1）-4（b+n），在数学中，我们把这种方法称为整体代换法，常常用这样的方法把复杂的问题转化为简单问题．
【灵活运用】应用整体代换法解答下列问题：
（1）已知t=-1，求代数式2（t²-t-1）-（t²-t-1）+3（t²-t-1）的值；
（2）已知
x
=
-
1
3
，求代数式3（3x²-2x）+4（-3x²+2x+1）-（3x²-2x）的值；
（3）计算：
2022
×
（
1
-
1
2
-
2
3
-
3
4
-…-
2020
2021
）
-
2023
×
（
1
+
1
2
+
1
3
+
1
4
+
…
+
1
2022
）
+
2023
×
（
1
+
1
2
+
1
3
+
1
4
+
…
+
1
2023
）
-
2022
×
（
1
-
1
2
-
2
3
-
3
4
-…-
2021
2022
）
．
组卷：97引用：2难度：0.6
解析
26．阅读下列两则材料：
材料1
君君同学在研究数学问题时遇到一个定义：对于按固定顺序排列的k个数：x₁，x₂，x₃，…，x_k，称为数列A_k：x₁，x₂，x₃，…，x_k，其中k为整数且k≥3．
定义：V（A_k）=|x₁-x₂|+|x₂-x₃|+…+|x_k-1-x_k|，
例如数列A₅：1，2，3，4，5，则V（A₅）=|1-2|+|2-3|+|3-4|+|4-5|=4．
材料2
有理数a,b在数轴上对应的两点A，B之间的距离是|a-b|；反之，|a-b|表示有理数a,b在数轴上对应点A，B之间的距离，我们称之为绝对值的几何意义．君君同学求|x-1|+|x+2|的最小值时，利用绝对值的几何意义表示在数轴上x对应点到1和-2对应点的距离之和，当-2≤x≤1时，取到它的最小值3，即为1和-2对应点之间的距离．
根据以上材料，回答下列问题：
（1）已知数列A₃：2，3，5，求V（A₃）；
（2）已知数列A₄：x₁，x₂，x₃，x₄，其中x₁，x₂，x₃，x₄为4个互不相等的整数，且x₁=3，x₄=6，V（A₄）=3，直接写出数列A₄：
；
（3）已知数列A₁：2，a,2，a+1，若V（A₄）=3，求a的值；
（4）已知数列A₅：x₁，x₂，x₃，x₄，x₅，5个数均为非负整数，且x₁+x₂+x₃+x₄+x₅=24，则V（A₅）的最小值是
．
组卷：67引用：2难度：0.5
解析