2022-2023学年北京市西城区高一（下）期末数学试卷

一、选择题共10小题，每小题4分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．

• 1．已知复数z满足z=1+i,则在复平面内

  z

  对应的点在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：118引用：2难度：0.8

  解析

• 2．下列函数中，最小正周期为π且是偶函数的是（　　）

  A． y = sin （ x + π 4 ）	B．y=tanx
  C．y=cos2x	D．y=sin2x
  组卷：278引用：5难度：0.7

  解析

• 3．在△ABC中，2a=b,C=60°，

  c

  =

  3

  ，则a=（　　）

  A． 1 2

  B．1

  C． 3

  D． 2 3
  组卷：327引用：1难度：0.8

  解析

• 4．某城市—年中12个月的月平均气温y（单位℃）与月份x（x=1，2，3，…，12）的关系可近似地用三角函数

  y

  =

  a

  +

  A

  sin

  [

  π

  6

  （

  x

  -

  3

  ）

  ]

  （

  A

  ＞

  0

  ）

  来表示，已知月平均气温最高值为28℃，最低值为18℃，则A=（　　）

  A．5

  B．10

  C．15

  D．20
  组卷：193引用：1难度：0.8

  解析

• 5．复数z=cosα+isinα，且z²为纯虚数，则α可能的取值为（　　）

  A．0

  B． π 4

  C． π 3

  D． π 2
  组卷：191引用：3难度：0.7

  解析

• 6．已知直线m,直线n和平面α，则下列四个命题中正确的是（　　）

  A．若m∥α，n⊂α，则m∥n	B．若m∥α，n∥α，则m∥n
  C．若m⊥α，n∥α，则m⊥n	D．若m⊥n,n∥α，则m⊥α
  组卷：586引用：6难度：0.7

  解析

• 7．在平面直角坐标系中，O为坐标原点，P（1，-2），Q（3，4），则cos∠POQ=（　　）

  A． 5 3

  B． 5 5

  C． - 5 3

  D． - 5 5
  组卷：265引用：3难度：0.7

  解析

三、解答题共6小题，共85分．解答应写出文字说明、演算步骤或证明过程．

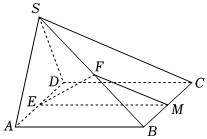• 20．如图，在四棱锥S-ABCD中，平面SAD⊥平面ABCD，SA=SD=AD=2，四边形ABCD为正方形，E为AD的中点，F为SB上一点，M为BC上一点，且平面EFM∥平面SCD．
  （1）求证：CD⊥SA；
  （2）求证：M为线段BC中点，并直接写出M到平面SCD的距离；
  （3）在棱SC上是否存在点N，使得平面DMN⊥平面ABCD？若存在，求

  CN

  CS

  ；若不存在，说明理由．
  组卷：285引用：2难度：0.5

  解析

• 21．对于定义在R上的函数f（x）和正实数T，若对任意x∈R，有f（x+T）-f（x）=T，则f（x）为T-阶梯函数．
  （1）分别判断下列函数是否为1-阶梯函数（直接写出结论）：
  ①f（x）=x²；②f（x）=x+1．
  （2）若f（x）=x+sinx为T-阶梯函数，求T的所有可能取值；
  （3）已知f（x）为T-阶梯函数，满足：f（x）在

  [

  T

  2

  ，

  T

  ]

  上单调递减，且对任意x∈R，有f（T-x）-f（x）=T-2x.若函数F（x）=f（x）-ax-b有无穷多个零点，记其中正的零点从小到大依次为x₁，x₂，x₃，…直接给出一个符合题意的a的值，并证明：存在b∈R，使得F（x）在[0，2023T]上有4046个零点，且x₂-x₁=x₃-x₂=…=x₄₀₄₆-x₄₀₄₅．
  组卷：89引用：4难度：0.3

  解析