2023-2024学年广东省惠州市六校高二（上）联考数学试卷（10月份）

一、选择题（本题共8小题，每小题满分40分，共40分。在每小题给出的四个选项中，只有一项符合题目要求，选对得5分，选错得0分）

• 1．下列说法不正确的是（　　）

  A．长方体是平行六面体	B．正方体是平行六面体
  C．直四棱柱是长方体	D．平行六面体是四棱柱
  组卷：125引用：4难度：0.5

  解析

• 2．若P（1，0，-2），Q（3，1，1）在直线l上，则直线l的一个方向向量为（　　）

  A．（1，2，3）

  B．（1，3，2）

  C．（2，1，3）

  D．（3，2，1）
  组卷：516引用：5难度：0.8

  解析

• 3．下列关于概率的命题，错误的是（　　）

  A．对于任意事件A，都有P（A）≥0

  B．必然事件的概率为1

  C．如果事件A与事件B对立，那么一定有P（A）+P（B）=1

  D．若A，B是一个随机试验中的两个事件，则P（A∪B）=P（A）+P（B）
  组卷：161引用：4难度：0.8

  解析

• 4．在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E、F、G、H分别为A₁B₁、B₁C₁、A₁D₁、BB₁的中点，则

  |

  GF

  +

  GH

  +

  2

  EG

  |

  =（　　）

  A． 6

  B． 2 6

  C． 3

  D． 2 3
  组卷：33引用：2难度：0.7

  解析

• 5．已知向量

  OA

  =

  （

  0

  ，

  1

  ，

  2

  ）

  ，

  OB

  =

  （

  -

  1

  ，

  0

  ，

  1

  ）

  ，

  OC

  =

  （

  2

  ，

  1

  ，

  λ

  ）

  ，若O，A，B，C共面，则

  OC

  在

  OB

  上的投影向量的模为（　　）

  A． 2 2

  B． 2

  C． 2 5 5

  D． 5 5
  组卷：325引用：10难度：0.7

  解析

• 6．在一个边长为2的等边三角形ABC中，若点P是平面ABC（包括边界）中的任意一点，则

  PA

  •

  PC

  的最小值是（　　）

  A． - 5 2

  B． - 4 3

  C．-1

  D． - 3 4
  组卷：67引用：3难度：0.7

  解析

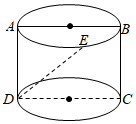• 7．我们打印用的A4纸的长与宽的比约为

  2

  ，之所以是这个比值，是因为把纸张对折，得到的新纸的长与宽之比仍约为

  2

  ，纸张的形状不变．已知圆柱的母线长小于底面圆的直径长（如图所示），它的轴截面ABCD为一张A4纸，若点E为上底面圆上弧

  ˆ

  AB

  的中点，则异面直线DE与AB所成的角约为（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 2 π 3
  组卷：276引用：8难度：0.8

  解析

四、解答题（共6小题，共70分。解答应写出文字说明、证明过程或演算步骤）。

• 21．已知△ABC中，内角A，B，C所对的边分别为a,b,c,且

  a

  +

  b

  -

  c

  b

  +

  c

  -

  a

  =

  1

  9

  ，

  a

  +

  b

  -

  c

  c

  +

  a

  -

  b

  =

  1

  5

  ．
  （1）若∠ACB的平分线与边AB交于点D，求

  AD

  c

  的值；
  （2）若a=2，点M，N分别在边AC，BC上，△CMN的周长为5，求MN的最小值．
  组卷：75引用：5难度：0.5

  解析

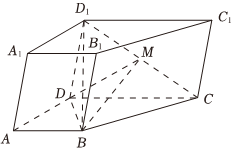• 22．如图，四棱柱ABCD-A₁B₁C₁D₁的底面ABCD为直角梯形，∠DAB=∠ADC=90°，AB=AD=1，CD=2，直线BD₁与直线CD所成的角取得最大值．点M为CD₁的中点，且CD₁=2BM．
  （1）证明：平面BDM⊥平面BD₁M；
  （2）若钝二面角B-DM-C的余弦值为

  -

  15

  15

  ，当BD₁＞BD时，求三棱锥D-BD₁M的体积．
  组卷：27引用：3难度：0.5

  解析