2023-2024学年重庆一中高二（上）月考数学试卷（9月份）

一、单项选择题（本大题共8个小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项符合要求的）

• 1．椭圆

  x

  2

  9

  +

  y

  2

  25

  =

  1

  与椭圆

  x

  2

  9

  -

  m

  +

  y

  2

  25

  -

  m

  =

  1

  （

  m

  ＜

  9

  ）

  的（　　）

  A．长轴相等

  B．短轴相等

  C．焦距相等

  D．长轴、短轴、焦距均不相等
  组卷：221引用：3难度：0.6

  解析

• 2．若方程

  x

  2

  25

  -

  m

  +

  y

  2

  m

  +

  9

  =

  1

  表示椭圆，则实数m的取值范围是（　　）

  A．（-9，25）	B．（-9，8）∪（8，25）
  C．（8，25）	D．（8，+∞）
  组卷：585引用：10难度：0.8

  解析

• 3．椭圆

  x

  2

  12

  +

  y

  2

  3

  =

  1

  的一个焦点为F₁，点P在椭圆上且在第一象限，如果线段PF₁的中点M在y轴上，那么点M的纵坐标是（　　）

  A． 3 4

  B． 3 2

  C． 2 2

  D． 3 4
  组卷：192引用：1难度：0.7

  解析

• 4．19世纪法国著名数学家加斯帕尔•蒙日，创立了画法几何学，推动了空间几何学的独立发展，提出了著名的蒙日圆定理：椭圆的两条切线互相垂直，则切线的交点位于一个与椭圆同心的圆上，称为蒙日圆，椭圆

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）的蒙日圆方程为x²+y²=a²+b²．若圆（x-3）²+（y-b）²=9与椭圆

  x

  2

  3

  +y²=1的蒙日圆有且仅有一个公共点，则b的值为（　　）

  A．3

  B．4

  C．5

  D．2 5
  组卷：299引用：7难度：0.6

  解析

• 5．设F₁、F₂分别是椭圆

  x

  2

  4

  +

  y

  2

  =

  1

  的左、右焦点，若Q是该椭圆上的一个动点，则

  Q

  F

  1

  •

  Q

  F

  2

  的最小值为（　　）

  A．2

  B．1

  C．-1

  D．-2
  组卷：324引用：2难度：0.5

  解析

• 6．已知在平面直角坐标系xOy中，圆C的方程为x²+y²=-2y+3，直线l经过点（1，0）且与直线x-y+1=0垂直，若直线l与圆C交于A，B两点，则△OAB的面积为（　　）

  A．1

  B． 2

  C．2

  D．2 2
  组卷：139引用：13难度：0.7

  解析

• 7．数学美的表现形式多种多样，我们称离心率e=ω（其中

  ω

  =

  5

  -

  1

  2

  ）的椭圆为黄金椭圆，现有一个黄金椭圆方程为

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  ，

  （

  a

  ＞

  b

  ＞

  0

  ）

  ，若以原点O为圆心，短轴长为直径作⊙O，P为黄金椭圆上除顶点外任意一点，过P作⊙O的两条切线，切点分别为A，B，直线AB与x,y轴分别交于M，N两点，则

  b

  2

  |

  OM

  |

  2

  +

  a

  2

  |

  ON

  |

  2

  =（　　）

  A． 1 ω

  B．ω

  C．-ω

  D． - 1 ω
  组卷：581引用：14难度：0.5

  解析

四、解答题（共70分.解答应写出必要的文字说明，证明过程或演算步骤）

• 21．已知在平面直角坐标系xOy中，A（0，1），B（0，4），平面内动点P满足2|PA|=|PB|．
  （1）求点P的轨迹方程；
  （2）点P轨迹记为曲线τ，若C，D是曲线τ与x轴的交点，E为直线l：x=4上的动点，直线CE，DE与曲线τ的另一个交点分别为M，N，直线MN与x轴交点为Q，求点Q的坐标．
  组卷：44引用：3难度：0.4

  解析

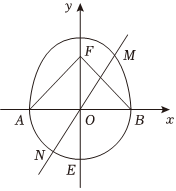• 22．如图，已知半圆C₁：x²+y²=b²（y≤0）与x轴交于A、B两点，与y轴交于E点，半椭圆C₂：

  y

  2

  a

  2

  +

  x

  2

  b

  2

  =1（y＞0，a＞b＞0）的上焦点为F，并且△ABF是面积为

  3

  的等边三角形，将由C₁、C₂构成的曲线，记为“Γ”．
  （1）求实数a、b的值；
  （2）直线l：y=

  2

  x与曲线Γ交于M、N两点，在曲线Γ上再取两点S、T（S、T分别在直线l两侧），使得这四个点形成的四边形MSNT的面积最大，求此最大面积；
  （3）设点K（0，t）（t∈R），P是曲线Γ上任意一点，求|PK|的最小值．
  组卷：423引用：7难度：0.2

  解析