2023-2024学年湖北省武汉市蔡甸区、黄陂区、江夏区九年级（上）期中数学试卷

一、选择题．（共10小题，每小题3分，共30分）

• 1．方程2x²-3x-1=0的二次项系数和一次项系数分别为（　　）

  A．2x2和-3x

  B．2x2和3x

  C．2和-3

  D．2和3
  组卷：95引用：2难度：0.8

  解析

• 2．若x₁、x₂是一元二次方程x²+3x-5=0的两根，则x₁+x₂的值是（　　）

  A．3

  B．-3

  C．5

  D．-5
  组卷：242引用：3难度：0.6

  解析

• 3．下列交通标志中，既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：39引用：1难度：0.9

  解析

• 4．抛物线y=2（x+7）²-5的顶点坐标是（　　）

  A．（7，-5）

  B．（-7，-5）

  C．（7，5）

  D．（-7，5）
  组卷：138引用：4难度：0.6

  解析

• 5．将抛物线y=x²向左平移2单位，再向上平移3个单位，则所得的抛物线解析式为（　　）

  A．y=（x+2）2+3

  B．y=（x-2）2+3

  C．y=（x+2）2-3

  D．y=（x-2）2-3
  组卷：382引用：15难度：0.9

  解析

• 6．如图，将△ABC绕顶点C逆时针旋转得到△A'B'C，且点B刚好落在A'B'上．若∠A=27°，∠BCA'=35°，则∠A'BA等于（　　）

  A．35°

  B．56°

  C．62°

  D．66°
  组卷：124引用：3难度：0.5

  解析

• 7．已知点A（a,2023）与点A′（2024，b）是关于原点O的对称点，则a-b的值为（　　）

  A．-1

  B．1

  C．-4047

  D．4047
  组卷：74引用：1难度：0.7

  解析

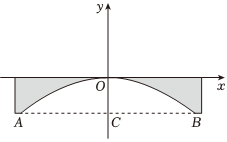• 8．某大桥的桥拱可以用抛物线的一部分表示，函数关系为

  y

  =

  -

  1

  25

  x

  2

  ，当水面宽度AB为20m时，水面与桥拱顶的高度CO等于（　　）

  A．2m

  B．4m

  C．10m

  D．16m
  组卷：694引用：6难度：0.8

  解析

三、解答题．（共72分）

• 23．问题背景
  如图1，△ABC与△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，求证：BD=CE；
  尝试应用
  如图2，点D是等边△ABC内一点，连接BD、CD，点E在BD上，ED=CD，延长CD交AE于F，若∠EDC=120°，求证：点F是AE的中点；
  拓展应用
  如图3，已知△ABC中，∠ABC=30°，

  AB

  =

  2

  3

  ，BC=9，以AC为底边在△ABC外作等腰三角形ACD，且∠ADC=120°，连接BD，则BD的长为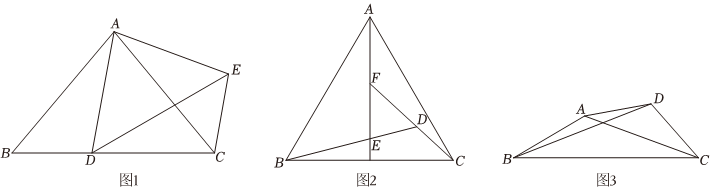

  ．
  
  组卷：369引用：2难度：0.2

  解析

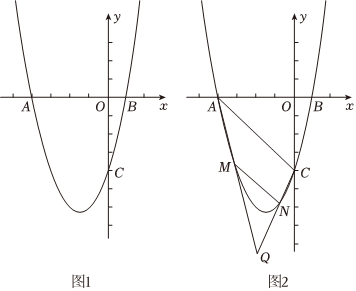• 24．如图1，已知二次函数y=x²+bx+c的图象与x轴交于点A（-4，0）和点B，与y轴的负半轴交于点C（0，-4）．
  （1）求这个函数的解析式；
  （2）点P是抛物线上的一点，当∠BCP=45°时，求点P的坐标；
  （3）如图2，将直线AC向下平移与抛物线交于M、N两点，直线AM、CN交于Q点，请问点Q的横坐标是否为定值，并说明理由．
  ​
  组卷：403引用：2难度：0.5

  解析